日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
已知四邊形ABCD是菱形，則(
AB
+
AD
)•(
AB
-
AD
)=（　　）
分析：由四邊形ABCD是菱形，可得
AB
2=
AD
2，由此求得 (
AB
+
AD
)•(
AB
-
AD
)=
AB
2-
AD
2 的值．
解答：解：∵已知四邊形ABCD是菱形，∴
AB
2=
AD
2．
∴(
AB
+
AD
)•(
AB
-
AD
)=
AB
2-
AD
2=0，
故選：A．
點評：本題主要考查兩個向量的數量積的運算，得到
AB
2=
AD
2，是解題的關鍵，屬于基礎題．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

17、如圖，已知四邊形ABCD 是矩形，PA⊥平面ABCD，M，N分別是AB，PC的中點．
（1）求證：MN∥平面PAD；
（2）求證：MN⊥DC．

查看答案和解析>>

科目：高中數學 來源： 題型：

某城市計劃在如圖所示的空地ABCD上豎一塊長方形液晶廣告屏幕MNEF，宣傳該城市未來十年計劃、目標等相關政策．已知四邊形ABCD是邊長為30m的正方形，電源在點P處，點P到邊AD、AB的距離分別為9m，3m，且MN～NE=16～9，線段MN必過點P，端點M、N分別在邊AD、AB上，設AN=xm，液晶廣告屏幕MNEF的面積為Sm2．
（1）求S關于x的函數關系式及其定義域；
（2）若液晶屏每平米造價為1500元，當x為何值時，液晶廣告屏幕MNEF的造價最低？

查看答案和解析>>

科目：高中數學 來源： 題型：

如圖，已知四邊形ABCD是菱形，PA⊥平面ABCD，PA=AB=BD=2，AC與BD交于E點，F是PD的中點．
（1）求證：PB∥平面AFC；
（2）求多面體PABCF的體積．

查看答案和解析>>

科目：高中數學 來源： 題型：

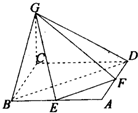如圖：已知四邊形ABCD是邊長為4的正方形，E、F分別是AB，AD的中點，GC垂直于ABCD所在平面，且GC=2．
（1）求異面直線BC與GE所成的角的余弦值；
（2）求平面CBG與平面BGD的夾角的余弦值；
（3）求三棱錐D-GEF的體積．

查看答案和解析>>

科目：高中數學 來源： 題型：

精英家教網已知四邊形ABCD是空間四邊形，E，F，G，H分別是邊AB，BC，CD，DA的中點，求證：四邊形EFGH是平行四邊形．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： av免费在线播放 | 午夜国产精品成人 | 久久久极品 | 久久久久国产一区二区三区四区 | 日本一区精品 | 日本五月婷婷 | 欧洲色| 国产欧美日韩综合精品一区二区 | 浴室洗澡偷拍一区二区 | 国产精品一区二区久久久 | 成人免费小视频 | 99精品一区二区 | 激情开心站 | 中文字幕在线视频观看 | 无码一区二区三区视频 | 国内久久 | 一区二区中文字幕在线观看 | 欧美极品一区二区三区 | 国内精品在线视频 | 91亚洲国产成人久久精品网站 | 欧美国产免费 | 欧美人成在线视频 | av大片在线观看 | 视频一区 中文字幕 | 中文字幕二区 | 国产欧美久久一区二区三区 | 日韩国产精品一区二区三区 | 精品一区二区三区免费 | 国产福利在线播放麻豆 | 视频一区二区国产 | 欧美一区二区免费 | 成人欧美一区二区三区在线播放 | jlzzxxxx18hd护士 | 久久全国免费视频 | 欧美一区二区三区精品免费 | 国产精品一二三四区 | 久久夜夜操妹子 | 色一情一乱一伦一区二区三区 | 亚洲一区高清 | 成人午夜视频在线观看 | 国产2区|