分析:(1)由f(x)=ax
3+bx
2-a
2x(a>0),知f'(x)=3ax
2+2bx-a
2(a>0)依題意有
,由此能求出f(x).
(2)先對函數進行求導,根據函數f(x)=ax
3+bx
2-a
2x(a>0)的兩個極值點為m,n(m≠n),可以得到△>0且由韋達定理可得m+n,mn,把等式轉化為關于m+n,mn的關系式,求出a、b的關系,把a看成未知數x,求三次函數的最值,利用導數求極值,是b
2最大值,開方可求b的最大值.
解答:解:(1)∵f(x)=ax
3+bx
2-a
2x(a>0),
∴f'(x)=3ax
2+2bx-a
2(a>0)
依題意有
,
∴
(a>0).
解得
,
∴f(x)=6x
3-9x
2-36x.
(2)∵f'(x)=3ax
2+2bx-a
2(a>0),
依題意,m,n是方程f'(x)=0的兩個根,
且|m|+|n|=2
,
∴(m+n)
2-2mn+2|mn|=8.
∴
(-)2-2•(-)+2|-|=8,
∴b
2=3a
2(6-a)
∵b
2≥0,
∴0<a≤6,
設p(a)=3a
2(6-a),
則p′(a)=-9a
2+36a.
由p'(a)>0得0<a<4,
由p'(a)<0得a>4.
即:函數p(a)在區間(0,4]上是增函數,
在區間[4,6]上是減函數,
∴當a=4時,p(a)有極大值為96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值為
4.
點評:本題考查函數解析式的求法和實數b的最大值的求法.由原函數極值點的個數判斷出導函數解的個數,利用判別式得參數的關系,用韋達定理把參數和解聯系起來,韋達定理是個很好的“橋梁”,求最大值要先求極大值,三次函數一般用導數來求.



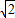 ,求b的最大值.
,求b的最大值.