某公司計劃2011年在甲、乙兩個電視臺做總時間不超過300分鐘的廣告，廣告費用不超過9萬元.甲、乙電視臺的廣告收費標準分別為500元/分鐘和200元/分鐘.假定甲、乙兩個電視臺為該公司每分鐘所做的廣告，能給公司帶來的收益分別為0.3 萬元和0.2萬元.問：該公司如何分配在甲、乙兩個電視臺的廣告時間，才能使公司收益最大，最大收益是多少萬元？
該公司在甲電視臺做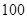
分鐘廣告，在乙電視臺做
分鐘廣告，公司的收益最大，最大收益是
萬元.
解析試題分析：由題意可知，若設公司在甲電視臺和乙電視臺做廣告的時間分別為
分鐘和
分鐘，總收益為
元，則可得
，
，從而問題就等價于在線性約束條件
下，求線性目標函數，作出不等式組所表示的可行域，在作出直線
，通過平移直線，即可知，使目標函數取得最大值的點為直線
與直線
的交點
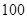，從而得到該公司在甲電視臺做分鐘廣告，在乙電視臺做分鐘廣告，公司的收益最大，最大收益是萬元.
試題解析：設公司在甲電視臺和乙電視臺做廣告的時間分別為分鐘和分鐘，總收益為元，由題意得：，， 6分
不等式組等價于，作出二元一次不等式組所表示的平面區域，即可行域，如圖：
作直線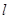
：
，即， 8分
平移直線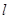，從圖中可知，當直線過點
時，目標函數取得最大值，
聯立
， 8分
∴點的坐標為，∴
（元）， 11分
∴該公司在甲電視臺做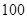分鐘廣告，在乙電視臺做分鐘廣告，公司的收益最大，最大收益是萬元.
考點：線性規劃的運用.
超能學典應用題題卡系列答案科目：高中數學 來源： 題型：解答題
(2013·黃山模擬)若x,y滿足約束條件
(1)求目標函數z=
x-y+的最值.
(2)若目標函數z=ax+2y僅在點(1,0)處取得最小值,求a的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某營養師要為某個兒童預訂午餐和晚餐，已知一個單位的午餐含
個單位的碳水化合物，
個單位的蛋白質和個單位的維生素
；一個單位的晚餐含
個單位的碳水化合物，個單位的蛋白質和
個單位的維生素.另外，該兒童這兩餐需要的營養中至少含
個單位的碳水化合物，
個單位的蛋白質和
個單位的維生素.如果一個單位的午餐、晚餐的費用分別是
元和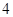
元，那么要滿足上述的營養要求，并且花費最少，應當為該兒童分別預訂多少個單位的午餐和晚餐？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
、
滿足約束條件
，則
的最大值為 
中，已知點
，
，
，點
在
三邊圍成的區域（含邊界）上，且
.
，求
；
表示
，并求
的最大值為 
則
的最大值是 ▲ 。
，式中變量
滿足下列條件:
則z的最大值為_____.
，若
，則實數
的取值范圍是（ ）
