
【題目】甲、乙兩陶瓷廠生產規格為![]() 的矩形瓷磚(長和寬都約為
的矩形瓷磚(長和寬都約為![]() ) ,根據產品出廠檢測結果,每片瓷磚質量
) ,根據產品出廠檢測結果,每片瓷磚質量![]() (單位:
(單位:![]() )在
)在![]() 之間的稱為正品,其余的作為廢品直接回爐處理.正品瓷
之間的稱為正品,其余的作為廢品直接回爐處理.正品瓷
磚按行業生產標準分為“優等”、“一級”、“合格”三個標準,主要按照每片瓷磚的“尺寸誤差”加以劃分,每片價格分別為![]() 元、
元、![]() 元、
元、![]() 元.若規定每片正品瓷磚的“尺寸誤差”計算方式為,設矩形瓷磚的長與寬分別為
元.若規定每片正品瓷磚的“尺寸誤差”計算方式為,設矩形瓷磚的長與寬分別為![]() (單位:
(單位:![]() ) ,則“尺寸誤差”為
) ,則“尺寸誤差”為![]() ,“優等”瓷磚的“尺寸誤差”范圍是
,“優等”瓷磚的“尺寸誤差”范圍是![]() ,“一級”瓷磚的“尺寸誤差”范圍是
,“一級”瓷磚的“尺寸誤差”范圍是![]() ,“合格”瓷磚的“尺寸誤差”范圍是
,“合格”瓷磚的“尺寸誤差”范圍是![]() .現分別從甲、乙兩廠生產的正品瓷磚中隨機抽取
.現分別從甲、乙兩廠生產的正品瓷磚中隨機抽取![]() 片瓷磚,相應的“尺寸誤差”組成的樣本數據如下:
片瓷磚,相應的“尺寸誤差”組成的樣本數據如下:
(甲廠產品的“尺寸誤差”頻數表)
尺寸誤差 | 頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(乙廠產品的“尺寸誤差”柱狀圖)

(1)根據樣本數據分別計算甲、乙兩廠生產的正品瓷磚的“尺寸誤差”的平均值;
(2)若用這個樣本的頻率分布估計總體分布,求乙廠所生產的正品瓷磚的平均價格;
(3)現用分層抽樣的方法從甲廠生產的![]() 片樣本瓷磚中隨機抽取
片樣本瓷磚中隨機抽取![]() 片,再從抽取的
片,再從抽取的![]() 片瓷磚中的“一級”瓷磚與“合格”瓷磚中隨機選.取
片瓷磚中的“一級”瓷磚與“合格”瓷磚中隨機選.取![]() 片進一步分析其“平整度”,求這
片進一步分析其“平整度”,求這![]() 片瓷磚的價格之和大于
片瓷磚的價格之和大于![]() 元的概率.
元的概率.
【答案】(1)0.225;(2)7.05;(3)![]() .
.
【解析】
(1)根據數據分別計算甲、乙兩廠生產的正品瓷磚的“尺寸誤差”的平均值即可.
(2)根據乙廠產品的“尺寸誤差”柱狀圖,計算正品瓷磚的平均價格即可.
(3)首先利用分層抽樣的方法分別求出“一級”瓷磚和“合格”瓷磚抽取的個數,再列舉出從中選取![]() 片的全部情況和價格之和大于
片的全部情況和價格之和大于![]() 元的情況,用古典概型公式計算即可.
元的情況,用古典概型公式計算即可.
(1)甲廠生產的正品瓷磚的“尺寸誤差”的平均值為:
![]() ,
,
乙廠生產的正品瓷磚的“尺寸誤差”的平均值為:
![]() .
.
(2)乙廠所生產的正品瓷磚的平均價格為:
![]() .
.
![]() 用分層抽樣的方法從甲廠生產的
用分層抽樣的方法從甲廠生產的![]() 片樣本瓷磚中隨機抽取
片樣本瓷磚中隨機抽取![]() 片,
片,
則“一級”瓷磚抽取![]() 片,記為
片,記為![]() ;
;
“合格”瓷磚抽取.![]() 片,記為
片,記為![]() ;
;
從中選取![]() 片有:
片有:![]() ,
,
![]() ,共
,共![]() 種選法,
種選法,
其中價格之和大于![]() 元,即選取的
元,即選取的![]() 片都為“一級”瓷磚的
片都為“一級”瓷磚的
有![]() 共
共![]() 種選法
種選法
所以選取的![]() 片瓷磚的價格之和大于
片瓷磚的價格之和大于![]() 元的概率
元的概率![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() .
.
(Ⅰ)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(Ⅱ)若橢圓![]() 的短軸長為
的短軸長為![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() :
: ![]() 滿足:
滿足: ![]() ,
, ![]() 或1(
或1(![]() ).對任意
).對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且兩兩不相等.
且兩兩不相等.
(I)若![]() .寫出下列三個數列中所有符合題目條件的數列的序號;
.寫出下列三個數列中所有符合題目條件的數列的序號;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)記![]() .若
.若![]() ,證明:
,證明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年7月,超強臺風登陸某地區.據統計,本次臺風造成該地區直接經濟損失119.52億元.經過調查住在該地某小區的50戶居民由于臺風造成的經濟損失,作出如下頻率分布直方圖:
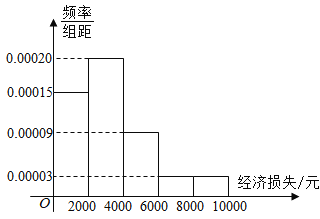
(1)根據頻率分布直方圖估計小區平均每戶居民的平均損失;
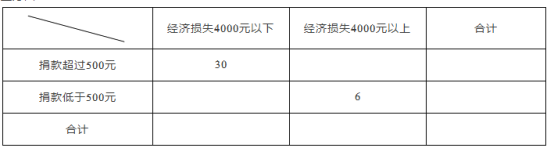
(2)臺風后區委會號召小區居民為臺風重災區捐款,經過調查的50戶居民捐款情況如下表,在表格空白處填寫正確數字,并說明是否有![]() 以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關?
以上的把握認為捐款數額是否多于或少于500元和自身經濟損失是否到4000元有關?
(3)臺風造成了小區多戶居民門窗損壞,若小區所有居民的門窗均由王師傅和張師傅兩人進行維修,王師傅每天早上在7:00到8:00之間的任意時刻來到小區,張師傅每天早上在7:30到8:30分之間的任意時刻來到小區,求王師傅比張師傅早到小區的概率.
附:臨界值表

參考公式: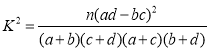 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均為正實數,且滿足a+b+c=m,求證:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 已知函數f(x)=|x+a|+|x-2|.
(1)當a=-3時,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com