2008年世界經濟出現嚴重衰退,我國政府為了刺激經濟增長,2009年開始加大貨幣貸款量,為一批中小企業解決資經短缺問題.某私營企業獲得一筆貸款準備新建一棟面積為10000m2,高為10m,底面為矩形的廠房,由于受地理環境的影響,矩形的一邊(南北方向)不能超過a(m),已知廠房的地面造價為800元/m2,頂的造價為500元/m2,墻壁的造價為600元/m2,設廠房南北方向長為x(m),造價為y(元).
(I)寫出用x(m)表示y(元)的函數關系式并指出定義域;
(II)求x為何值時廠房的造價最低,并求出最低價.
解:(I)根據題設,南北方向的邊長為xm,0<x≤a,
則寬為:
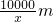
,矩形的周長為W,
那么W=2(x+

,墻的面積為10W=20(x+

)
[所以y=8000000+5000000+12000
y=13000000+12000(x

)
其定義域為x∈(0,a]
(II)由(I)y=13000000+12000(x+

)
①a≥100時,y≥1300000+2400

=1540000
∴顯然當

=
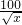
即x=100時
y
min=15400000
②當0<a<100時
設x
1<x
2<a
(x
2+
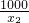
)-(x
1+
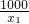
)
=(x2-x1)
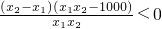
∴y=13000000+12000(x+
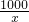
)
在區間(0,a]上是減函數
則當x=a時,y取最小值y
min=13000000+12000(a+
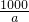
)
故當a≥100時
y
min=15400000元
當0<a<100時,ymin=1300000+12000(a+
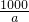
)
分析:(I)根據題意,設出南北方向的邊長,直接寫出用x(m)表示y(元)的函數關系式.
(II)分別分a≥100時以及0<a<100時,根據基本不等式與函數單調性求出最值.
點評:本題考查函數模型的選取與應用,通過對實際問題的分析,轉化為函數表達式,通過對基本不等式的運用求解最值,考查學生對知識的熟練運用能力,屬于中檔題.

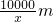 ,矩形的周長為W,
,矩形的周長為W, ,墻的面積為10W=20(x+
,墻的面積為10W=20(x+ )
) )
) )
) =1540000
=1540000 =
=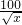
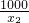 )-(x1+
)-(x1+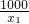 )
)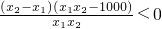
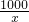 )
)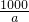 )
)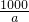 )
)
