解答:(Ⅰ)證明:因?yàn)?span id="p9vv5xb5" class="MathJye">AC=2
,PA=2,PE=2EC,
故
PC=2,EC=,F(xiàn)C=,
從而
=,=.
因?yàn)?span id="p9vv5xb5" class="MathJye">
=
,∠FCE=∠PCA,
所以△FCE∽△PCA,∠FEC=∠PAC=90°,
由此知PC⊥EF. …(5分)
(Ⅱ)證明:因?yàn)榈酌鍭BCD為菱形,所以BD⊥AC.
又PA⊥底面ABCD,所以PC⊥BD.
由(Ⅰ)知PC⊥EF,所以PC與平面BED內(nèi)兩條相交直線BD,EF都垂直,
所以PC⊥平面BED.
因?yàn)锽E、ED在平面平面BED內(nèi),所以EB⊥PC,ED⊥PC,所以∠BED是二面角B-PC-D的平面角. …(9分)
(Ⅲ)解:在平面PAB內(nèi)過(guò)點(diǎn)A作AG⊥PB,G為垂足.
因?yàn)槎娼茿-PB-C為90°,所以平面PAB⊥平面PBC.
又平面PAB∩平面PBC=PB.
故AG⊥平面PBC,AG⊥BC.
所以BC與平面PAB內(nèi)兩條相交直線PA,AG都垂直,故BC⊥平面PAB,
于是BC⊥AB,
所以底面ABCD為正方形,
AD=2,PD==2. …(11分)
設(shè)D到平面PBC的距離為d.
因?yàn)锳D∥BC,且AD?平面PBC,BC?平面PBC,
故AD∥平面PBC,A、D兩點(diǎn)到平面PBC的距離相等,即
d=AG=.
設(shè)PD與平面PBC所成的角為α,則
sina==.
所以PD與平面PBC所成的角為30°. …(14分)

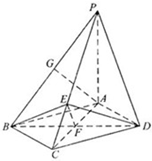
 已知四棱錐P-ABCD中,底面ABCD為菱形,PA⊥底面ABCD,底面ABCD的對(duì)角線的交點(diǎn)為F,AC=2
已知四棱錐P-ABCD中,底面ABCD為菱形,PA⊥底面ABCD,底面ABCD的對(duì)角線的交點(diǎn)為F,AC=2



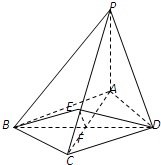
 如圖,已知四棱錐P--ABC的底面ABCD為正方形,PA⊥平面ABCD,PA=AB=2,e為PC的中點(diǎn),F(xiàn)為AD的中點(diǎn).
如圖,已知四棱錐P--ABC的底面ABCD為正方形,PA⊥平面ABCD,PA=AB=2,e為PC的中點(diǎn),F(xiàn)為AD的中點(diǎn). 如圖,已知四棱錐P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,側(cè)面PBC⊥底面ABCD,O是BC的中點(diǎn).
如圖,已知四棱錐P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,側(cè)面PBC⊥底面ABCD,O是BC的中點(diǎn). 已知四棱錐P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E為BC中點(diǎn),AE與BD交于O點(diǎn),AB=BC=2CD=2,BD⊥PE.
已知四棱錐P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E為BC中點(diǎn),AE與BD交于O點(diǎn),AB=BC=2CD=2,BD⊥PE. 如圖,已知四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是線段PC上一點(diǎn),PC⊥平面BDE.
如圖,已知四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是線段PC上一點(diǎn),PC⊥平面BDE.