
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的方程為
的方程為![]() ,且圓
,且圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,設直線
兩點,設直線![]() 的方程為
的方程為![]() .
.
(1)當直線![]() 與圓
與圓![]() 相切時,求直線
相切時,求直線![]() 的方程;
的方程;
(2)已知直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點.(i)
兩點.(i)![]() ,求直線
,求直線![]() 的方程;(ii)直線
的方程;(ii)直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,直線
,直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,是否存在常數
,是否存在常數![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)![]() ;(2)(i)直線
;(2)(i)直線![]() 的方程為
的方程為![]() ;(ii)存在常數
;(ii)存在常數![]() ,使得
,使得![]() 恒成立.
恒成立.
【解析】
(1)利用圓心到直線的距離等于半徑構造關于![]() 的方程,解方程求得結果;(2)(i)設
的方程,解方程求得結果;(2)(i)設![]() ,由
,由![]() 可得
可得![]() ,代入圓的方程可求解出
,代入圓的方程可求解出![]() 點坐標,從而得到斜率,求得直線方程;(ii)將直線
點坐標,從而得到斜率,求得直線方程;(ii)將直線![]() 方程代入圓的方程可求得
方程代入圓的方程可求得![]() 點坐標;同理將直線
點坐標;同理將直線![]() 方程代入圓的方程可求得
方程代入圓的方程可求得![]() 點坐標;利用
點坐標;利用![]() 可求得
可求得![]() 的關系,利用
的關系,利用![]() 表示出
表示出![]() 點坐標,整理可得
點坐標,整理可得![]() ,進而可得到
,進而可得到![]() 滿足
滿足![]() ,得到常數
,得到常數![]() .
.
(1)由題意,![]()
![]() 圓心
圓心![]() 到直線
到直線![]() 的距離
的距離![]()
![]() 直線
直線![]() 與圓
與圓![]() 相切
相切 ![]() ,解得:
,解得:![]()
![]() 直線
直線![]() 方程為:
方程為:![]()
(2)(i)設![]() ,由
,由![]() 得:
得:![]()
由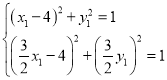 ,解得:
,解得: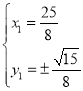
![]()
![]() 直線
直線![]() 的方程為:
的方程為:![]()
(ii)由題意知:![]() ,
,![]()
則![]() ,與圓
,與圓![]() 聯立得:
聯立得:![]()
![]()
![]()
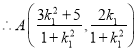
同理可得: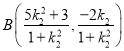
![]()
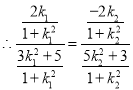 ,整理可得:
,整理可得:![]()
![]()
![]()
設![]()
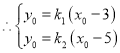

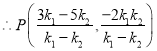 ,即
,即![]()
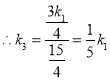
![]()
![]() 存在常數
存在常數![]() ,使得
,使得![]() 恒成立
恒成立


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩人參加一個射擊的中獎游戲比賽,在相同條件下各打靶50次,統計每次打靶所得環數,得下列頻數分布表.
環數 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的頻數 | 0 | 1 | 4 | 7 | 14 | 16 | 6 | 2 |
乙的頻數 | 1 | 2 | 5 | 6 | 10 | 16 | 8 | 2 |
比賽中規定所得環數為1,2,3,4時獲獎一元,所得環數為5,6,7時獲獎二元,所得環數為8,9時獲獎三元,所得環數為10時獲獎四元,沒命中則無獎.
(1)根據上表,在答題卡給定的坐標系內畫出甲射擊50次獲獎金額(單位:元)的條形圖;

(2)估計甲射擊1次所獲獎至少為三元的概率;
(3)要從甲、乙兩人中選拔一人參加射擊比賽,請你根據甲、乙兩人所獲獎金額的平均數和方差作出選擇.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,C、D是離心率為![]() 的橢圓的左、右頂點,
的橢圓的左、右頂點,![]() 、
、![]() 是該橢圓的左、右焦點, A、B是直線
是該橢圓的左、右焦點, A、B是直線![]() 4上兩個動點,連接AD和BD,它們分別與橢圓交于點E、F兩點,且線段EF恰好過橢圓的左焦點
4上兩個動點,連接AD和BD,它們分別與橢圓交于點E、F兩點,且線段EF恰好過橢圓的左焦點![]() . 當
. 當![]() 時,點E恰為線段AD的中點.
時,點E恰為線段AD的中點.
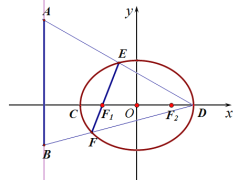
(Ⅰ)求橢圓的方程;
(Ⅱ)求證:以AB為直徑的圓始終與直線EF相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖都是由邊長為1的正方體疊成的幾何體,例如第(1)個幾何體的表面積為6個平方單位,第(2)個幾何體的表面積為18個平方單位,第(3)個幾何體的表面積是36個平方單位.依此規律,則第![]() 個幾何體的表面積是__________個平方單位.
個幾何體的表面積是__________個平方單位.
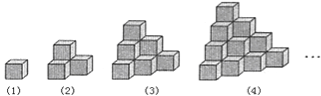
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】研究機構對某校學生往返校時間的統計資料表明:該校學生居住地到學校的距離![]() (單位:千米)和學生花費在上學路上的時間
(單位:千米)和學生花費在上學路上的時間![]() (單位:分鐘)有如下的統計資料:
(單位:分鐘)有如下的統計資料:
到學校的距離 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花費的時間 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統計資料表明![]() 與
與![]() 有線性相關關系,試求:
有線性相關關系,試求:
(1)判斷![]() 與
與![]() 是否有很強的線性相關性?
是否有很強的線性相關性?
(相關系數![]() 的絕對值大于0.75時,認為兩個變量有很強的線性相關性,精確到0.01)
的絕對值大于0.75時,認為兩個變量有很強的線性相關性,精確到0.01)
(2)求線性回歸方程![]() (精確到0.01);
(精確到0.01);
(3)將![]() 分鐘的時間數據
分鐘的時間數據![]() 稱為美麗數據,現從這6個時間數據
稱為美麗數據,現從這6個時間數據![]() 中任取2個,求抽取的2個數據全部為美麗數據的概率.
中任取2個,求抽取的2個數據全部為美麗數據的概率.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
參考公式: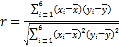 ,
,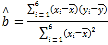
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】菜市房管局為了了解該市市民2018年1月至2019年1月期間購買二手房情況,首先隨機抽樣其中200名購房者,并對其購房面積![]() (單位:平方米,
(單位:平方米,![]() )進行了一次調查統計,制成了如圖1所示的頻率分布南方匿,接著調查了該市2018年1月﹣2019年1月期間當月在售二手房均價
)進行了一次調查統計,制成了如圖1所示的頻率分布南方匿,接著調查了該市2018年1月﹣2019年1月期間當月在售二手房均價![]() (單位:萬元/平方米),制成了如圖2所示的散點圖(圖中月份代碼1﹣13分別對應2018年1月至2019年1月).
(單位:萬元/平方米),制成了如圖2所示的散點圖(圖中月份代碼1﹣13分別對應2018年1月至2019年1月).
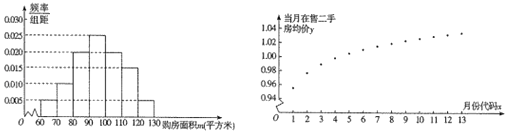
(1)試估計該市市民的平均購房面積![]() .
.
(2)現采用分層抽樣的方法從購房耐積位于![]() 的40位市民中隨機取4人,再從這4人中隨機抽取2人,求這2人的購房面積恰好有一人在
的40位市民中隨機取4人,再從這4人中隨機抽取2人,求這2人的購房面積恰好有一人在![]() 的概率.
的概率.
(3)根據散點圖選擇![]() 和
和![]() 兩個模型進行擬合,經過數據處理得到兩個回歸方程,分別為
兩個模型進行擬合,經過數據處理得到兩個回歸方程,分別為![]() 和
和![]() ,并得到一些統計量的值,如表所示:
,并得到一些統計量的值,如表所示:
|
| |
|
|
|
|
| |
請利用相關指數![]() 判斷哪個模型的擬合效果更好,并用擬合效果更好的模型預測2019年6月份的二手房購房均價(精確到
判斷哪個模型的擬合效果更好,并用擬合效果更好的模型預測2019年6月份的二手房購房均價(精確到
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .參考公式:相關指數
.參考公式:相關指數 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確命題的個數是( )
①對于命題![]() ,使得
,使得![]() ,則
,則![]() ,均有
,均有![]() ;
;
②命題“已知x,![]() ,若
,若![]() ,則
,則![]() 或
或![]() ”是真命題;
”是真命題;
③設![]() ,
,![]() 是非零向量,則“
是非零向量,則“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
④![]() 是直線
是直線![]() 與直線
與直線![]() 互相垂直的充要條件.
互相垂直的充要條件.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com