
![]()
(1)如果分別以t,α為參數,則所給的參數方程表示的圖象分別是什么?請分別把它們轉化為普通方程.(α為參數時,設t>0,t為參數時,設α≠![]() )
)
(2)求上述直線截上述曲線所得的弦長.
(3)根據上述求解過程總結出一個結論,并用基本語句編寫一個算法計算弦長.
思路分析:本題綜合考查參數方程,直線與曲線的位置關系以及算法等基本知識.首先根據參數方程的形式知:當t為參數時,參數方程表示直線,當α為參數表示圓,且直線恰好過圓的圓心,所以弦長就是圓的直徑.根據所給的參數方程不難得到一般結論,用算法表示弦長只需根據數據求出圓的直徑,所以只需使用順序結構即可.
解:(1)以t為參數時,所給參數方程表示的圖形是過點(2,5)且斜率為tanα的直線,化為普通方程是y-5=tanα(x-2);
以t為參數時,參數方程表示以(2,5)為圓心,半徑為t的圓,化為普通方程是(x-2)2+(y-5)2=t2.
(2)上述直線恰好過圓的圓心,所以截圓所得弦長為圓的直徑2t.
(3)根據上述計算過程可以總結出一般的結論為:對于一個參數方程
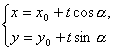 (α為參數時,設t>0,t為參數時,設α≠
(α為參數時,設t>0,t為參數時,設α≠![]() ),如果分別以t,α為參數,則所給的參數方程表示的圖象分別是一條直線和一個圓,且直線過圓的圓心,所以直線截圓所得弦長是圓的直徑2t.
),如果分別以t,α為參數,則所給的參數方程表示的圖象分別是一條直線和一個圓,且直線過圓的圓心,所以直線截圓所得弦長是圓的直徑2t.
用基本語句寫出表示弦長的算法如下:
INPUT“參數t(t>0)”;t,
d=2t,
PRINT“所給參數方程表示的直線被圓截得的弦長是”;d,
END.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
 在A、B、C、D四小題中只能選做2題,每小題10分,共計20分.請在答題紙指定區域內 作答.解答應寫出文字說明、證明過程或演算步驟.
在A、B、C、D四小題中只能選做2題,每小題10分,共計20分.請在答題紙指定區域內 作答.解答應寫出文字說明、證明過程或演算步驟.
|
|
|
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省鹽城中學高三(上)12月月考數學試卷(解析版) 題型:解答題
 在A、B、C、D四小題中只能選做2題,每小題10分,共計20分.請在答題紙指定區域內 作答.解答應寫出文字說明、證明過程或演算步驟.
在A、B、C、D四小題中只能選做2題,每小題10分,共計20分.請在答題紙指定區域內 作答.解答應寫出文字說明、證明過程或演算步驟.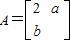 屬于特征值-1的一個特征向量為
屬于特征值-1的一個特征向量為 ,求矩陣A的逆矩陣.
,求矩陣A的逆矩陣. (t為參數,t∈{R}).試求曲線C上點M到直線l的距離的最大值.
(t為參數,t∈{R}).試求曲線C上點M到直線l的距離的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com