Question

假設p、q都是奇數,求證:關于x的方程x²+px+q=0無整數根.

      

Answer 1

思路分析:此題中含有否定詞“無”,可考慮用反證法,另外關于有無整數根,可從已知方程的判別式與根和系數的關系入手分析證明之.?

       證法一:只有在Δ=p²-4q=(p-m)²時〔(p-m)²表示完全平方數,其中由-4q=-2pm+m²可知m應為偶數〕才可能有整數根.化簡上式得出p與q的關系:q=p·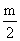-(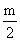)²,因p是奇數,不論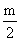是怎樣的整數,都可得q為偶數,這與已知q為奇數相矛盾,則判別式Δ的值不會是一個完全平方數,故方程無整數根.?

       證法二:假設方程有整數根α,無論α是奇數還是偶數,都必有α²+pα+q為奇數,這與

α²+pα+q=0矛盾.故方程無整數根.