
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,當
,當![]() 時,求
時,求![]() 的最大值.
的最大值.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在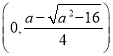 ,
,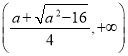 上單調遞增;在
上單調遞增;在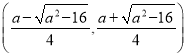 上單調遞減;
上單調遞減;
(2)![]()
【解析】
(1)先對函數![]() 求導,分別討論
求導,分別討論![]() 和
和![]() ,即可得出結果;
,即可得出結果;
(2)先由(1)得到![]() ,
,![]() ,對
,對![]() 化簡整理,再令
化簡整理,再令![]() ,得到
,得到![]() ,根據(1)和
,根據(1)和![]() 求出
求出![]() 的范圍,再令
的范圍,再令![]() ,用導數的方法求其最大值,即可得出結果.
,用導數的方法求其最大值,即可得出結果.
(1)由![]() 得
得![]() ;
;
因為![]() ,所以
,所以![]() ;
;
因此,當![]() 時,
時,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,由
時,由![]() 得
得![]() ,解得
,解得![]() 或
或![]() ;由
;由![]() 得
得![]() ;
;
所以![]() 在
在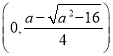 ,
,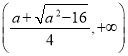 上單調遞增;在
上單調遞增;在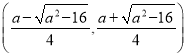 上單調遞減;
上單調遞減;
綜上,當![]() 時,
時,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在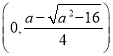 ,
,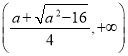 上單調遞增;在
上單調遞增;在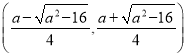 上單調遞減;
上單調遞減;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,
,
由(1)可得, ![]() 是方程
是方程![]() 的兩不等實根,
的兩不等實根,
所以![]() ,
,![]() ,
,
因此![]()
![]() ,
,
令![]() ,則
,則![]() ;
;
由(1)可知![]() ,
,
當![]() 時,
時,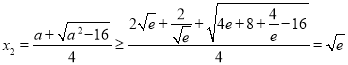 ,
,
所以![]() ,
,
令![]() ,
,![]() ,
,
則![]() 在
在![]() 上恒成立;
上恒成立;
所以![]() 在
在![]() 上單調遞減,
上單調遞減,
故![]() .
.
即![]() 的最大值為
的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某人某天的工作是:駕車從![]() 地出發,到
地出發,到![]() 兩地辦事,最后返回
兩地辦事,最后返回![]() 地,
地,![]() 三地之間各路段行駛時間及當天降水概率如下表:
三地之間各路段行駛時間及當天降水概率如下表:
路段 | 正常行駛所需時間(小時) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,則在該路段行駛的時間需延長1小時.
現有如下兩個方案:
方案甲:上午從![]() 地出發到
地出發到![]() 地辦事,然后到達
地辦事,然后到達![]() 地, 下午在
地, 下午在![]() 地辦事后返回
地辦事后返回![]() 地;
地;
方案乙:上午從![]() 地出發到
地出發到![]() 地辦事,下午從
地辦事,下午從![]() 地出發到達
地出發到達![]() 地,辦事后返回
地,辦事后返回![]() 地.設此人8點從
地.設此人8點從![]() 地出發,在各地辦事及午餐的累積時間為2小時.
地出發,在各地辦事及午餐的累積時間為2小時.
現采用隨機數表法獲取隨機數并進行隨機模擬試驗,按照以下隨機數表,以方框內的數字5為起點,從左向右依次讀取數據,若到達某行最后一個數字,則從下一行最左側數字繼續讀取,每次讀取4位隨機數,第1位數表示采取的方案,其中0-4表示采用方案甲,5-9表示采用方案乙;第2-4位依次分別表示當天行駛的三個路段上是否降水,若某路段降水概率為![]() ,則
,則![]() 表示降水,
表示降水,![]() 表示不降水.(符號
表示不降水.(符號![]() 表示的數集包含
表示的數集包含![]() )
)
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23099842 99 64 61 71 6299 15 06![]() 1 29 169358 05 77 05 91
1 29 169358 05 77 05 91
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(1)利用數據“5129”模擬當天的情況,試推算他當日辦完事返回![]() 地的時間;
地的時間;
(2)利用隨機數表依次取出采用甲、乙方案的模擬結果各兩組,分別計算甲、乙兩個方案的平均時間,并回答哪個方案辦完事后能盡早返回![]() 地.
地.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年10月1日是新中國的第70個國慶日,莊重的閱兵、歡樂的游行、熱烈的聯歡盡顯祖國的繁榮昌盛.為了了解當天某校900名高三學生的觀看情況,從中抽取了100名學生,情況如下表所示:
觀看情況 | 電視觀看 | 網絡觀看 | 沒有觀看 |
人數 | 35 | 60 | 5 |
新時代下,網絡觀看使用最多的是手機,其它還有電腦、ipad等.“是否使用手機觀看”與“學生的性別”之間對應的列聯表如下:
使用手機觀看 | 其它方式觀看 | 合計 | |
男學生 | 20 | 8 | 28 |
女學生 | 20 | 12 | 32 |
合計 | 40 | 20 | 60 |
(1)估計該校高三學生當天的觀看人數.
(2)當天沒有觀看的5名學生中,有3人第二天觀看了重播.從這5名學生中任選2人求這2人第二天都看了重播的概率;
(3)根據列聯表判斷,能否有95%的把握認為網絡觀看的學生中“是否使用手機觀看”與“學生的性別”有關?
附: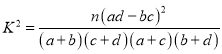 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() 為
為![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() ,連結
,連結![]() ,
,![]() 為
為![]() 的中點,則在翻折過程中,下列說法中所有正確的是( )
的中點,則在翻折過程中,下列說法中所有正確的是( )
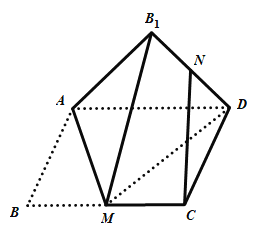
A.存在某個位置,使得![]()
B.翻折過程中,![]() 的長是定值
的長是定值
C.若![]() ,則
,則![]()
D.若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,三棱錐
的體積最大時,三棱錐![]() 的外接球的表面積是
的外接球的表面積是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 是我國古代著名數學經典
是我國古代著名數學經典![]() 其中對勾股定理的論述比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小
其中對勾股定理的論述比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小![]() 以鋸鋸之,深一寸,鋸道長一尺
以鋸鋸之,深一寸,鋸道長一尺![]() 問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深一寸,鋸道長一尺
問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深一寸,鋸道長一尺![]() 問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示
問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示![]() 陰影部分為鑲嵌在墻體內的部分
陰影部分為鑲嵌在墻體內的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌在墻中的體積約為( )(注:1丈
寸,估算該木材鑲嵌在墻中的體積約為( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直角坐標系![]() 中,點
中,點![]() 到拋物線
到拋物線![]() 的準線的距離為
的準線的距離為![]() ,點
,點![]() 是
是![]() 上的定點,
上的定點,![]() 、
、![]() 是
是![]() 上的兩個動點,且線段
上的兩個動點,且線段![]() 的中點
的中點![]() 在線段
在線段![]() 上.
上.
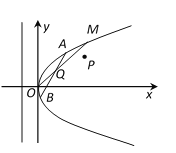
(1)拋物線![]() 的方程及
的方程及![]() 的值;
的值;
(2)當點![]() 、
、![]() 分別在第一、四象限時,求
分別在第一、四象限時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com