
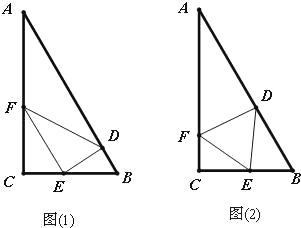
【題目】某公園有個池塘,其形狀為直角△ABC,![]() ,AB的長為2百米,BC的長為1百米.
,AB的長為2百米,BC的長為1百米.
(1)若準備養一批供游客觀賞的魚,分別在AB、BC、CA上取點D、E、F,如圖(1),使得![]() ,
,![]() ,在△DEF內喂食,求當△DEF的面積取最大值時EF的長;
,在△DEF內喂食,求當△DEF的面積取最大值時EF的長;
(2)若準備建造一個荷塘,分別在AB、BC、CA上取點D、E、F,如圖(2),建造△DEF連廊(不考慮寬度)供游客休憩,且使△DEF為正三角形,記![]() ,求△DEF邊長的最小值及此時
,求△DEF邊長的最小值及此時![]() 的值.(精確到1米和0.1度)
的值.(精確到1米和0.1度)
【答案】(1)![]() ;(2)最小值是65米,
;(2)最小值是65米,![]()
【解析】
(1)設EF=x,則可求CE,BE,DE,求得S△DEF![]() x(1
x(1![]() ),x∈(0,2),由基本不等式可得:
),x∈(0,2),由基本不等式可得:![]() (1
(1![]() )
)![]() (
(![]() )2當且僅當x=1時等號成立,從而可求當△DEF的面積取最大值時EF的長;
)2當且僅當x=1時等號成立,從而可求當△DEF的面積取最大值時EF的長;
(2)設等邊三角形邊長為EF=ED=DF=y,在△EBD中,由正弦定理及三角函數的性質可得y![]() 0.65,即可求得△DEF邊長的最小值及此時α的值.
0.65,即可求得△DEF邊長的最小值及此時α的值.
(1)設![]() ,則
,則![]() ,故
,故![]() ,所以
,所以![]() ,S△DEF
,S△DEF![]() ,
,![]() ,
,
因為S△DEF![]() 當且僅當
當且僅當![]() (即EF長100米)時等號成立,
(即EF長100米)時等號成立,
即(S△DE)max![]() .
.
(2)設等邊三角形邊長為![]() ,在△EBD中,
,在△EBD中,![]() ,
,![]() ,
,
由題意可知![]() ,則
,則![]() ,所以
,所以![]() ,
,
即![]() ,即△DEF邊長的最小值是65米,
,即△DEF邊長的最小值是65米,
此時![]() ,
,![]() ,
,![]()


 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數學 來源: 題型:
【題目】記無窮數列![]() 的前
的前![]() 項中最大值為
項中最大值為![]() ,最小值為
,最小值為![]() ,令
,令![]() .
.
(1)若![]() ,寫出
,寫出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)設![]() ,若
,若![]() ,求
,求![]() 的值及
的值及![]() 時數列
時數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)求證:“數列![]() 是等差數列”的充要條件是“數列
是等差數列”的充要條件是“數列![]() 是等差數列”.
是等差數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】七巧板是古代中國勞動人民發明的一種中國傳統智力玩具,它由五塊等腰直角三角形,一塊正方形和一塊平行四邊形共七塊板組成.清陸以湉《冷廬雜識》卷一中寫道:近又有七巧圖,其式五,其數七,其變化之式多至千余.體物肖形,隨手變幻,蓋游戲之具,足以排悶破寂,故世俗皆喜為之.如圖是一個用七巧板拼成的正方形,若在此正方形中任取一點,則此點取自陰影部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ;直線
;直線![]() 的參數方程為
的參數方程為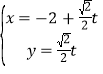 (t為參數).直線
(t為參數).直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若點![]() 的極坐標為
的極坐標為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:只要
滿足:只要![]() ,必有
,必有![]() ,則稱
,則稱![]() 具有性質
具有性質![]() .
.
(1)若![]() 具有性質
具有性質![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若無窮數列![]() 是等差數列,無窮數列
是等差數列,無窮數列![]() 是公比為正數的等比數列,
是公比為正數的等比數列, ![]() ,
, ![]() ,
, ![]() 判斷
判斷![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(3)設![]() 是無窮數列,已知
是無窮數列,已知![]() .求證:“對任意
.求證:“對任意![]() 都具有性質
都具有性質![]() ”的充要條件為“
”的充要條件為“![]() 是常數列”.
是常數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
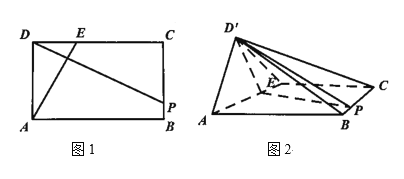
【題目】如圖1,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,現將
,現將![]() 沿
沿![]() 折到
折到![]() 的位置,連結
的位置,連結![]() ,
,![]() ,如圖2
,如圖2
(1)證明:![]() ;
;
(2)記平面![]() 與平面
與平面![]() 的交線為
的交線為![]() .若二面角
.若二面角![]() 為
為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,兩個焦點與短軸一個頂點構成等腰直角三角形,過點
,兩個焦點與短軸一個頂點構成等腰直角三角形,過點![]() 且與x軸不重合的直線l與橢圓交于M,N不同的兩點.
且與x軸不重合的直線l與橢圓交于M,N不同的兩點.
(Ⅰ)求橢圓P的方程;
(Ⅱ)當AM與MN垂直時,求AM的長;
(Ⅲ)若過點P且平行于AM的直線交直線![]() 于點Q,求證:直線NQ恒過定點.
于點Q,求證:直線NQ恒過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com