
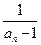 = bn,
= bn, }是等比數(shù)列 ⑵判斷{an}是否為無(wú)窮數(shù)列。
}是等比數(shù)列 ⑵判斷{an}是否為無(wú)窮數(shù)列。 +
+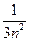 )<
)< ;
;  +
+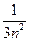 )<
)< ,證明略。
,證明略。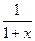 -1=
-1=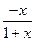 ,
,| x | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | 極大值 | ↘ |
 ,∴an+1-1=
,∴an+1-1=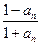 ,∴
,∴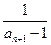 =-1-
=-1-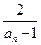 ,……………………5分
,……………………5分 =-2(bn+
=-2(bn+ ), b1+
), b1+ ="1,"
="1,"  }是首項(xiàng)為1,公比為-2的等比數(shù)列,…………………7分
}是首項(xiàng)為1,公比為-2的等比數(shù)列,…………………7分 =(-2)n-1, ……………………8分
=(-2)n-1, ……………………8分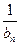 +1=
+1=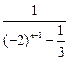 +1,……………………9分
+1,……………………9分 <-2, ∴an>0>-1恒成立,
<-2, ∴an>0>-1恒成立, +
+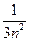 )< ln(1+
)< ln(1+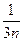 )3……………………12分
)3……………………12分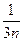 )≤3×
)≤3×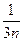 =
= 成立。 ………14分
成立。 ………14分


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
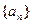 滿足
滿足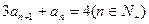 ,且
,且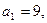 前n項(xiàng)和為
前n項(xiàng)和為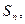 則滿足不等式
則滿足不等式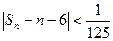 的最小整數(shù)n是( )
的最小整數(shù)n是( )| A.5 | B.6 | C.7 | D.8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
| A.9 | B.10 | C.11 | D.12 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
 和等比數(shù)列
和等比數(shù)列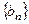 中,已知
中,已知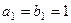 ,
, ,
, ;
;  的公差
的公差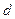 和
和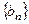 的公比
的公比 ;
;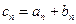 ,求數(shù)列
,求數(shù)列 的通項(xiàng)公式
的通項(xiàng)公式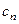 及前
及前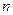 項(xiàng)和
項(xiàng)和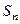 .
.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com