
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為矩形,側面
為矩形,側面![]() 為正三角形,
為正三角形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 為棱
為棱![]() 上一點(不與
上一點(不與![]() 、
、![]() 重合),平面
重合),平面![]() 交棱
交棱![]() 于點
于點![]() .
.
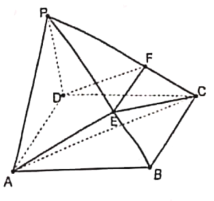
(1)求證:![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)先根據線面平行判定定理得![]() 平面
平面![]() ,再根據線面平行性質定理得結果;
,再根據線面平行性質定理得結果;
(2)取![]() 的中點
的中點![]() ,根據面面垂直性質定理得
,根據面面垂直性質定理得![]() 平面
平面![]() ,再根據條件建立空間直角坐標系,設立各點坐標,利用向量數量積解得平面
,再根據條件建立空間直角坐標系,設立各點坐標,利用向量數量積解得平面![]() 的一個方向量,再利用向量夾角公式以及二面角與向量夾角關系列方程,解得E點坐標,最后根據向量求點面距,即得結果.
的一個方向量,再利用向量夾角公式以及二面角與向量夾角關系列方程,解得E點坐標,最后根據向量求點面距,即得結果.
(1)![]() 底面
底面![]() 為矩形,
為矩形,![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .
.
![]() 側面
側面![]() 為正三角形,
為正三角形,![]() .
.
![]() 平面
平面![]() 平面
平面![]() 且交線為
且交線為![]() ,
,
![]() 平面
平面![]() ,
,![]() 為矩形,
為矩形,![]() ,
,![]() ,
,
![]() 如圖所示,建立以
如圖所示,建立以![]() ,
,![]() ,
,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 軸,
軸,![]() 軸的空間直角坐標系
軸的空間直角坐標系![]()
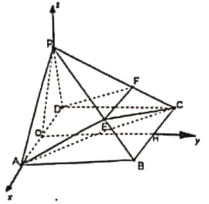
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
設![]() ,又
,又![]() ,
,![]() .
.
![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]()
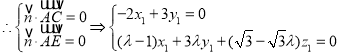 ,
,
令![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() 的一個法向量
的一個法向量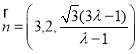 .
.
又易知![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
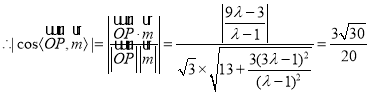 ,
,
解得:![]() ,
,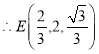 ,
,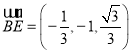 .
.
又![]() 平面
平面![]() 的一個法向量
的一個法向量![]() ,
,
![]() 點
點![]() 到平面
到平面![]() 的距離為:
的距離為: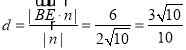 .
.


科目:高中數學 來源: 題型:
【題目】把一個均勻的正方體骰子拋擲兩次,觀察出現的點數,記第一次出現的點數為![]() ,第二次出現的點數為
,第二次出現的點數為![]() ,設直線
,設直線![]() :
:![]() ,直線
,直線![]() :
:![]() .
.
(1)求直線![]() 和直線
和直線![]() 沒有交點的概率;
沒有交點的概率;
(2)求直線![]() 和直線
和直線![]() 的交點在第一象限的概率.
的交點在第一象限的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 數列
數列![]() 的前
的前![]() 項和,對任意
項和,對任意![]() ,都有
,都有![]() (
(![]() 為常數).
為常數).
(1)當![]() 時,求
時,求![]() ;
;
(2)當![]() 時,
時,
(ⅰ)求證:數列![]() 是等差數列;
是等差數列;
(ⅱ)若數列![]() 為遞增數列且
為遞增數列且![]() ,設
,設![]() ,試問是否存在正整數
,試問是否存在正整數![]() (其中
(其中![]() ),使
),使![]() 成等比數列?若存在,求出所有滿足條件的數組
成等比數列?若存在,求出所有滿足條件的數組![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)令![]()
①當![]() 時,求函數
時,求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
②若![]() 時,
時,![]() 恒成立,求
恒成立,求![]() 的所有取值集合與
的所有取值集合與![]() 的關系;
的關系;
(Ⅱ)記![]() ,是否存在
,是否存在![]() ,使得對任意的實數
,使得對任意的實數![]() ,函數
,函數![]() 在
在![]() 上有且僅有兩個零點?若存在,求出滿足條件的最小正整數
上有且僅有兩個零點?若存在,求出滿足條件的最小正整數![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為直角梯形,
中,底面ABCD為直角梯形,![]() ,
,![]() 且
且![]() ,
,![]() 平面ABCD.
平面ABCD.
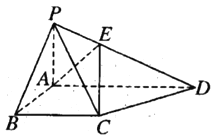
(1)求PA與平面PCD所成角的正弦值;
(2)棱PD上是否存在一點E,滿足![]() ?若存在,求AE的長;若不存在,說明理由.
?若存在,求AE的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,橢圓上的點到左焦點的最小值為
,橢圓上的點到左焦點的最小值為![]() .
.
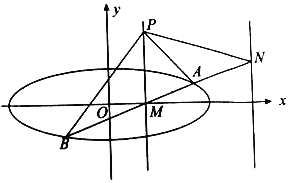
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 與
與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 為直線
為直線![]() 上任意一點,設直線
上任意一點,設直線![]() 與直線
與直線![]() 交于點
交于點![]() ,記
,記![]() ,
,![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,則是否存在實數
,則是否存在實數![]() ,使得
,使得![]() 恒成立?若是,請求出
恒成立?若是,請求出![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學界的震動.在1859年,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想.在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論.若根據歐拉得出的結論,估計10000以內的素數的個數為(素數即質數,
的結論.若根據歐拉得出的結論,估計10000以內的素數的個數為(素數即質數,![]() ,計算結果取整數)
,計算結果取整數)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著城市地鐵建設的持續推進,市民的出行也越來越便利.根據大數據統計,某條地鐵線路運行時,發車時間間隔t(單位:分鐘)滿足:4≤t≤15,![]() N,平均每趟地鐵的載客人數p(t)(單位:人)與發車時間間隔t近似地滿足下列函數關系:
N,平均每趟地鐵的載客人數p(t)(單位:人)與發車時間間隔t近似地滿足下列函數關系: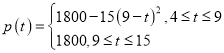 ,其中
,其中![]() .
.
(1)若平均每趟地鐵的載客人數不超過1500人,試求發車時間間隔t的值.
(2)若平均每趟地鐵每分鐘的凈收益為![]() (單位:元),問當發車時間間隔t為多少時,平均每趟地鐵每分鐘的凈收益最大?井求出最大凈收益.
(單位:元),問當發車時間間隔t為多少時,平均每趟地鐵每分鐘的凈收益最大?井求出最大凈收益.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com