
【題目】如圖三棱柱![]() 中,側面
中,側面![]() 為菱形,
為菱形, ![]() .
.
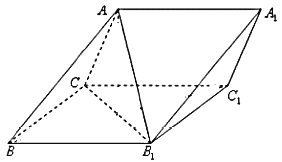
(1)證明: ![]() ;
;
(2)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,可證
,可證![]() 平面
平面![]() ,可得
,可得![]() ,
, ![]() ,進而可得
,進而可得![]() ;(2)以
;(2)以![]() 為坐標原點,
為坐標原點, ![]() 的方向為
的方向為![]() 軸正方向,
軸正方向, ![]() 為單位長,建立空間直角坐標系,分別可得兩平面的法向量,可得所求余弦值.
為單位長,建立空間直角坐標系,分別可得兩平面的法向量,可得所求余弦值.
試題解析:(1)連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,因為側面
,因為側面![]() 為菱形,所以
為菱形,所以![]() ,且
,且![]() 為
為![]() 及
及![]() 的中點,又
的中點,又![]() ,所以
,所以![]() 平面
平面![]() .由于
.由于![]() 平面
平面![]() ,故
,故![]() ,又
,又![]() ,故
,故![]() .
.
(2)因為![]() ,且
,且![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
又因為![]() ,所以
,所以![]() ,故
,故![]() ,從而
,從而![]() 兩兩相互垂直,
兩兩相互垂直, ![]() 為坐標原點,
為坐標原點, ![]() 的方向為
的方向為![]() 軸正方向,
軸正方向, ![]() 為單位長,建立空間直角坐標系
為單位長,建立空間直角坐標系![]() (圖略)
(圖略)
因為![]() ,所以
,所以![]() 為等邊三角形,又
為等邊三角形,又![]() ,則
,則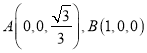 ,
, 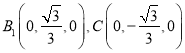 .
. 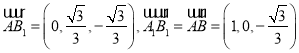 ,
, 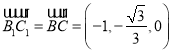 ,設
,設![]() 是平面
是平面![]() 的法向量,則
的法向量,則
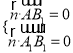 ,即
,即 ,設
,設![]() 是平面
是平面![]() 的法向量,則
的法向量,則 ,同理可取
,同理可取![]() .
.
所以可取![]() ,
, ![]() ,
,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(Ⅲ)設斜率為![]() 的直線與函數
的直線與函數![]() 的圖象交于
的圖象交于![]() ,
, ![]() 兩點,其中
兩點,其中![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】宋元時期杰出的數學家朱世杰在其數學巨著《四元玉鑒》卷中“茭草形段”第一個問題“今有茭草六百八十束,欲令‘落一形’埵(同垛)之.問底子(每層三角形邊茭草束數,等價于層數)幾何?”中探討了“垛枳術”中的落一形垛(“落一形”即是指頂上1束,下一層3束,再下一層6束,…,成三角錐的堆垛,故也稱三角垛,如圖,表示第二層開始的每層茭草束數),則本問題中三角垛底層茭草總束數為 .
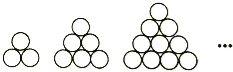
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中點,
的中點, ![]() 是
是![]() 上的點且
上的點且![]() 為
為![]() 邊
邊![]() 上的高.
上的高.
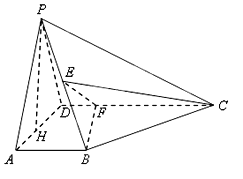
(1)證明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱錐
,求三棱錐![]() 的體積;
的體積;
(3)在線段![]() 上是否存在這樣一點
上是否存在這樣一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,說出
?若存在,說出![]() 點的位置.
點的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的準線
的準線![]() 與
與![]() 軸交于橢圓
軸交于橢圓![]() 的右焦點
的右焦點![]() 為
為![]() 的左焦點.橢圓的離心率為
的左焦點.橢圓的離心率為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 交于
交于![]() 軸上方一點
軸上方一點![]() ,連接
,連接![]() 并延長其交
并延長其交![]() 于點
于點![]() ,
, ![]() 為
為![]() 上一動點,且在
上一動點,且在![]() 之間移動.
之間移動.
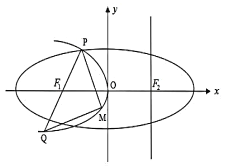
(1)當![]() 取最小值時,求
取最小值時,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的邊長恰好是三個連續的自然數,當
的邊長恰好是三個連續的自然數,當![]() 面積取最大值時,求面積最大值以及此時直線
面積取最大值時,求面積最大值以及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設O為坐標原點,點P的坐標(x﹣2,x﹣y)
(1)在一個盒子中,放有標號為1,2,3的三張卡片,現從此盒中有放回地先后抽到兩張卡片的標號分別記為x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;
(2)若利用計算機隨機在[0,3]上先后取兩個數分別記為x,y,求P點在第一象限的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,離心率為
,離心率為![]() ,設直線
,設直線![]() 的斜率是
的斜率是![]() ,且
,且![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓的標準方程.
(Ⅱ)若直線![]() 在
在![]() 軸上的截距是
軸上的截距是![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
(Ⅲ)以![]() 為底作等腰三角形,頂點為
為底作等腰三角形,頂點為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com