【題目】部分與整體以某種相似的方式呈現(xiàn)稱為分形.謝爾賓斯基三角形是一種分形，由波蘭數(shù)學家謝爾賓斯基1915年提出.具體操作是取一個實心三角形，沿三角形的三邊中點連線，將它分成4個小三角形，去掉中間的那一個小三角形后，對其余3個小三角形重復上述過程逐次得到各個圖形，如圖.
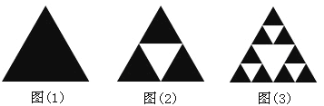
現(xiàn)在上述圖(3)中隨機選取一個點，則此點取自陰影部分的概率為_________.
科目：高中數(shù)學 來源： 題型：
【題目】對于曲線
所在的平面上的定點
，若存在以點為頂點的角
，使得
對于曲線上的任意兩個不同的點
恒成立，則稱角
為曲線的“點視角”，并稱其中最小的“點視角”為曲線相對于點的”點確視角”.已知曲線
和圓
是
軸上一點
（1）對于坐標原點
，寫出曲線的“點確視角”的大小；
（2）若
在曲線上，求
的最小值；
（3）若曲線和圓
的“點確視角”相等，求點坐標.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，
（1）當
時，求函數(shù)
的單調(diào)區(qū)間；
（2）設函數(shù)
，若
，且
在
上恒成立，求
的取值范圍；
（3）設函數(shù)
，若
，且
在
上存在零點，求的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】七巧板是古代中國勞動人民發(fā)明的一種中國傳統(tǒng)智力玩具，它由五塊等腰直角三角形，一塊正方形和一塊平行四邊形共七塊板組成.清陸以湉《冷廬雜識》卷一中寫道：近又有七巧圖，其式五，其數(shù)七，其變化之式多至千余.體物肖形，隨手變幻，蓋游戲之具，足以排悶破寂，故世俗皆喜為之.如圖是一個用七巧板拼成的正方形，若在此正方形中任取一點，則此點取自陰影部分的概率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的離心率為
，以橢圓的短軸為直徑的圓與直線
相切.
（Ⅰ）求橢圓
的方程；
（Ⅱ）設橢圓過右焦點
的弦為
、過原點的弦為
，若
，求證：
為定值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
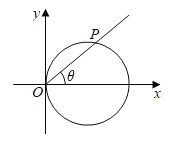
【題目】（1）如圖，以過原點的直線的傾斜角
為參數(shù)，求圓
的參數(shù)方程；
（2）在平面直角坐標系中，已知直線
的參數(shù)方程為
，（
為參數(shù)），曲線
的參數(shù)方程為
（
為參數(shù)），若與相交于
兩點，求
的長.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】過拋物線y2＝4x焦點F的直線交拋物線于A、B兩點，交其準線于點C，且A、C位于x軸同側(cè)，若|AC|＝2|AF|，則|BF|等于（ ）
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】從某企業(yè)生成的產(chǎn)品生產(chǎn)線上隨機抽取
件產(chǎn)品，測量這批產(chǎn)品的一項質(zhì)量指標值，由測量結(jié)果得如圖所示的頻率分布直方圖：
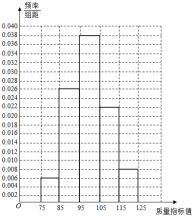
（1）估計這批產(chǎn)品質(zhì)量指標值的樣本平均
和樣本方差
（同一組中的數(shù)據(jù)用該組區(qū)間的中點值做代表）：
（2）若該種產(chǎn)品的等級及相應等級產(chǎn)品的利潤（每件）參照以下規(guī)則（其中
為產(chǎn)品質(zhì)量指標值）：當
該產(chǎn)品定為一等品，企業(yè)可獲利元；當
且
該產(chǎn)品定為二等品，企業(yè)可獲利
元：當
且
．該產(chǎn)品定為三等品，企業(yè)將損失
元；否則該產(chǎn)品定為不合格品，企業(yè)將損失
元
（i）若測得一箱產(chǎn)品（
件）的質(zhì)量指標數(shù)據(jù)分別為：
，求該箱產(chǎn)品的利潤；
（ii）設事件
；事件
事件
根據(jù)經(jīng)驗，對于該生產(chǎn)線上的產(chǎn)品，事件
發(fā)生的概率分別為
，根據(jù)以上信息，若產(chǎn)品預計年產(chǎn)量為
件，試估計設產(chǎn)品年獲利情況（參考數(shù)據(jù)：
）
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
