
【題目】已知函數![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線
處的切線![]() 與
與![]() 有且只有一個公共點,求
有且只有一個公共點,求![]() 的值;
的值;
(2)求證:函數![]() 存在單調遞減區間
存在單調遞減區間![]() ,并求出單調遞減區間的長度
,并求出單調遞減區間的長度![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】2018年2月9-25日,第23屆冬奧會在韓國平昌舉行.4年后,第24屆冬奧會將在中國北京和張家口舉行.為了宣傳冬奧會,某大學在平昌冬奧會開幕后的第二天,從全校學生中隨機抽取了120名學生,對是否收看平昌冬奧會開幕式情況進行了問卷調查,統計數據如下:
收看 | 沒收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根據上表說明,能否有![]() 的把握認為,收看開幕式與性別有關?
的把握認為,收看開幕式與性別有關?
(Ⅱ)現從參與問卷調查且收看了開幕式的學生中,采用按性別分層抽樣的方法選取8人,參加2022年北京冬奧會志愿者宣傳活動.
(ⅰ)問男、女學生各選取多少人?
(ⅱ)若從這8人中隨機選取2人到校廣播站開展冬奧會及冰雪項目宣傳介紹,求恰好選到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是城市慢行系統的一種創新模式,對于解決民眾出行“最后一公里”的問題特別見效,由于停取方便、租用價格低廉,各色共享單車受到人們的熱捧.某自行車廠為共享單車公司生產新樣式的單車,已知生產新樣式單車的固定成本為20 000元,每生產一輛新樣式單車需要增加投入100元.根據初步測算,自行車廠的總收益(單位:元)滿足分段函數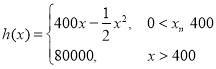 其中x是新樣式單車的月產量(單位:輛),利潤=總收益-總成本.
其中x是新樣式單車的月產量(單位:輛),利潤=總收益-總成本.
(1)試將自行車廠的利潤y元表示為月產量x的函數;
(2)當月產量為多少件時自行車廠的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
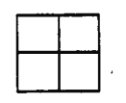
【題目】如圖,記從“田字型”網格(由四個邊長為1的正方形構成)的九個交點中任取三點構成的三角形面積為ξ(當所取的三點共線時,ξ=0),則ξ的數學期望![]() =_________。
=_________。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查全市學生的數學高考成績,隨機地抽取某中學甲、乙兩班各10名同學,獲得成績數據如下(單位:分).
甲:132,108,112,121,113,121,118,128,118,129;
乙:133,107,120,113,122,114,128,118,129,127.
(1)畫出甲、乙兩班學生數學成績的莖葉圖,并根據莖葉圖判斷哪個班的平均水平較高;
(2)若數學成績不低于120分,則稱為“優秀”,求從這20名學生中隨機選取三人,至多有一人是優秀的概率;
(3)以這20人的樣本數據來估計整個學校的總體成績,若從該校(人數很多)任選三人,記![]() 表示抽到優秀學生的人數,求
表示抽到優秀學生的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,根據長期收益率市場預測,投資債券等穩健型產品的收益與投資額成正比,投資股票等風險型產品的收益與投資額的算術平方根成正比.已知投資1萬元時兩類產品的收益分別為0.125萬元和0.5萬元。
(1)分別寫出兩類產品的收益與投資額的函數關系式;
(2)該家庭現有20萬元資金,全部用于理財投資,怎樣分配資金才能獲得最大收益?其最大收益為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】先后2次拋擲一枚骰子,將得到的點數分別記為![]() ,
,![]() .
.
(1)求直線![]() 與圓
與圓![]() 相切的概率;
相切的概率;
(2)將![]() ,
,![]() ,5的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
,5的值分別作為三條線段的長,求這三條線段能圍成等腰三角形的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com