
【題目】已知函數![]() ,且函數
,且函數![]() 在
在![]() 處取到極值.
處取到極值.
(1)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() ,且函數
,且函數![]() 有3個極值點
有3個極值點![]() ,
,![]() ,
,![]()
![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)證明見解析
;(2)證明見解析
【解析】
(1)求出原函數的導函數,由![]() 求解
求解![]() 值,則曲線
值,則曲線![]() 在
在![]() 處的切線方程可求;
處的切線方程可求;
(2)求出函數![]() 的解析式,由
的解析式,由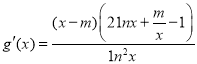 ,根據已知
,根據已知![]() 有
有
三個解,![]() 存在兩個不同于
存在兩個不同于![]() 的零點, 設
的零點, 設![]() ,求出
,求出![]() 取值范圍,結合
取值范圍,結合![]() 的函數特征,可判斷
的函數特征,可判斷![]() 是函數
是函數![]() 的兩個零點,構造函數
的兩個零點,構造函數![]() ,研究
,研究![]() 的單調性,把證明
的單調性,把證明![]() 轉化為證明
轉化為證明![]() 即可.
即可.
(1)![]() ,
,![]() ,
,
![]() 函數
函數![]() 在
在![]() 處取到極值,
處取到極值,![]() ,即
,即![]() .
.
則![]() ,
,![]() ,
,
∴曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ;
;
(2)![]() ,
,
函數的定義域為![]() 且
且![]() ,
,
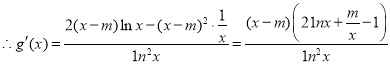
令![]() ,
,![]() ,
,
![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
![]() 是
是![]() 的最小值;
的最小值;![]() 有三個極值點
有三個極值點![]() ,
,
![]() ,得
,得![]() .
.
![]() 的取值范圍為
的取值范圍為![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,
![]() ;即
;即![]() ,
,![]() 是函數
是函數![]() 的兩個零點.
的兩個零點.
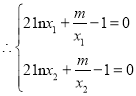 ,消去
,消去![]() 得
得![]() ;
;
令![]() ,
,![]() ,
,
![]() 的零點為
的零點為![]() ,且
,且![]() .
.
![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
要證明![]() ,即證
,即證![]() ,
,
等價于證明![]() ,即
,即![]() .
.
![]() ,
,![]() 即證
即證![]() .
.
構造函數![]() ,則
,則![]() ;
;
![]() 只要證明在
只要證明在![]() 上
上![]() 單調遞減,
單調遞減,
函數![]() 在
在![]() 單調遞減;
單調遞減;
![]() 增大時,
增大時,![]() 減小,
減小,![]() 增大,
增大,![]() 減小,
減小,
![]() 在
在![]() 上是減函數.
上是減函數.
![]() 在
在![]() 上是減函數.
上是減函數.
![]() 當
當![]() 時,
時,![]() .
.
即![]() .
.


科目:高中數學 來源: 題型:
【題目】若1路、2路公交車均途經泉港一中校門口,其中1路公交車每10分鐘一趟,2路公交車每20分鐘一趟,某生去坐這2趟公交車回家,則等車不超過5分鐘的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,斜率為1的直線與橢圓
,斜率為1的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 且與直線
且與直線![]() 平行的直線與橢圓
平行的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 滿足
滿足![]() ,且
,且![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于漸近線方程為![]() 的雙曲線有下述四個結論:①實軸長與虛軸長相等,②離心率是
的雙曲線有下述四個結論:①實軸長與虛軸長相等,②離心率是![]() ③過焦點且與實軸垂直的直線被雙曲線截得的線段長與實軸長相等,④頂點到漸近線與焦點到漸近線的距離比值為
③過焦點且與實軸垂直的直線被雙曲線截得的線段長與實軸長相等,④頂點到漸近線與焦點到漸近線的距離比值為![]() .其中所有正確結論的編號( )
.其中所有正確結論的編號( )
A.①②B.①③C.①②③D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,且
兩點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 上的一個動點,且直線
上的一個動點,且直線![]() 與直線
與直線![]() 分別交于
分別交于![]() 兩點.是否存在點
兩點.是否存在點![]() 使得以
使得以![]() 為直徑的圓經過點
為直徑的圓經過點![]() ?若存在,求出點
?若存在,求出點![]() 的橫坐標;若不存在,說明理由.
的橫坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產甲、乙兩種桶裝產品.已知生產甲產品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生產乙產品1桶需耗
原料2千克;生產乙產品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克.每桶甲產品的利潤是300元,每桶乙產品的利潤是400元.公司在生產這兩種產品的計劃中,要求每天消耗
原料1千克.每桶甲產品的利潤是300元,每桶乙產品的利潤是400元.公司在生產這兩種產品的計劃中,要求每天消耗![]() 原料都不超過12千克.通過合理安排生產計劃,從每天生產的甲、乙兩種產品中,公司共可獲得的最大利潤是__________元.
原料都不超過12千克.通過合理安排生產計劃,從每天生產的甲、乙兩種產品中,公司共可獲得的最大利潤是__________元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com