已知數列{bn}中,b1=1,且點(bn+1,bn)在直線y=x-1上.數列{an}中,a1=1,an+1=2an+3,
(Ⅰ) 求數列{bn}的通項公式
(Ⅱ)求數列{an}的通項公式;
(Ⅲ)若cn=an+3,求數列{bncn}的前n項和Sn.
【答案】
分析:(Ⅰ)利用點(b
n+1,b
n)在直線y=x-1上,確定數列{b
n}是以1為首項,1為公差的等差數列,可求數列{b
n}的通項公式;
(Ⅱ)根據數列遞推式a
n+1=2a
n+3,可得a
n+1+3=2(a
n+3),從而可得{a
n+3}是以4為首項,2為公比的等比數列,由此可求數列{a
n}的通項公式;
(Ⅲ)確定數列的通項,利用錯位相減法,可得數列{b
nc
n}的前n項和S
n.
解答:解:(Ⅰ)∵點(b
n+1,b
n)在直線y=x-1上,∴b
n+1-b
n=1
∵b
1=1,∴數列{b
n}是以1為首項,1為公差的等差數列
∴b
n=n(n∈N
*);
(Ⅱ)∵a
n+1=2a
n+3,∴a
n+1+3=2(a
n+3)
∵a
1=1,∴a
1+3=4
∴{a
n+3}是以4為首項,2為公比的等比數列
∴a
n+3=4×2
n-1=2
n+1,
∴
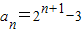
(n∈N
*);
(Ⅲ)c
n=a
n+3=2
n+1,∴b
nc
n=n×2
n+1,
∴S
n=1×2
2+2×2
3+…+n×2
n+1,①
∴2S
n=1×2
3+2×2
4+…+n×2
n+2,②
①-②可得:-S
n=1×2
2+1×2
3+…+1×2
n+1-n×2
n+2
∴
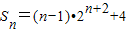
(n∈N
*)
點評:本題考查數列遞推式,考查數列通項的確定,考查數列的求和,確定數列是等差數列與等比數列是解題的關鍵.

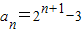 (n∈N*);
(n∈N*);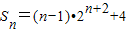 (n∈N*)
(n∈N*)

 ,
, ,數列{an}滿足:
,數列{an}滿足: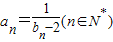 .
.