設f(n)=nn+1,g(n)=(n+1)n,n∈N*.
(1)當n=1,2,3,4時,比較f(n)與g(n)的大小.
(2)根據(1)的結果猜測一個一般性結論,并加以證明.
【答案】
分析:本題考查的知識點是歸納推理與數學歸納法,我們可以列出n
n+1與(n+1)
n(n∈N
*)的前若干項,然后分別比較其大小,然后由歸納推理猜想出一個一般性的結論,然后利用數學歸納法進行證明.
解答:解:(1)當n=1時,n
n+1=1,(n+1)
n=2,此時,n
n+1<(n+1)
n,
當n=2時,n
n+1=8,(n+1)
n=9,此時,n
n+1<(n+1)
n,
當n=3時,n
n+1=81,(n+1)
n=64,此時,n
n+1>(n+1)
n,
當n=4時,n
n+1=1024,(n+1)
n=625,此時,n
n+1>(n+1)
n,
(2)根據上述結論,我們猜想:當n≥3時,n
n+1>(n+1)
n(n∈N
*)恒成立.
①當n=3時,n
n+1=3
4=81>(n+1)
n=4
3=64
即n
n+1>(n+1)
n成立.
②假設當n=k時,k
k+1>(k+1)
k成立,即:
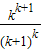
>1
則當n=k+1時,
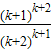
=
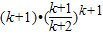
>
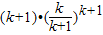
=
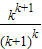
>1
即(k+1)
k+2>(k+2)
k+1成立,即當n=k+1時也成立,
∴當n≥3時,n
n+1>(n+1)
n(n∈N
*)恒成立.
點評:數學歸納法常常用來證明一個與自然數集N相關的性質,其步驟為:設P(n)是關于自然數n的命題,若1)(奠基) P(n)在n=1時成立;2)(歸納) 在P(k)(k為任意自然數)成立的假設下可以推出P(k+1)成立,則P(n)對一切自然數n都成立.

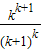 >1
>1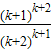 =
=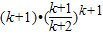 >
>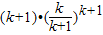 =
=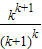 >1
>1

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案