
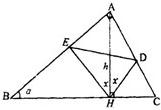
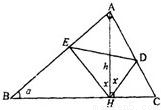
 如圖∠A=90°,∠B=α,AH=h,α,h為常數,AH⊥BC于H,∠AHE=∠AHD=x,問當x取何值時,△DEH的面積最大?并求出最大面積.
如圖∠A=90°,∠B=α,AH=h,α,h為常數,AH⊥BC于H,∠AHE=∠AHD=x,問當x取何值時,△DEH的面積最大?并求出最大面積. | π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| h | ||
sin(
|
| EH | ||
sin(
|
| hcosα |
| cos(α-x) |
| hsinα |
| sin(α+x) |
| 1 |
| 2 |
| 1 |
| 2 |
| hcosα |
| cos(α-x) |
| hsinα |
| sin(α+x) |
| 1 |
| 2 |
| ||
|
| 1 |
| 4 |
| sin 22α |
| sin2α+sin2x |
| π |
| 4 |
| 1 |
| 4 |
| sin 22α |
| sin2α+1 |
| π |
| 4 |
| 1 |
| 4 |
| sin 22α |
| sin2α+1 |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
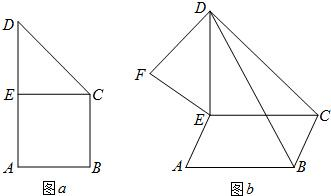 如圖a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=
如圖a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
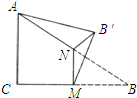 如圖∠C=90°,AC=BC,M,N分別為BC和AB的中點,沿直線MN將△BMN折起,使二面角B'-MN-B為60°,則斜線B'A與平面ABC所成角的正切值為
如圖∠C=90°,AC=BC,M,N分別為BC和AB的中點,沿直線MN將△BMN折起,使二面角B'-MN-B為60°,則斜線B'A與平面ABC所成角的正切值為
| ||
| 5 |
| ||
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
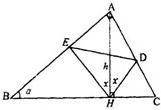 如圖∠A=90°,∠B=α,AH=h,α,h為常數,AH⊥BC于H,∠AHE=∠AHD=x,問當x取何值時,△DEH的面積最大?并求出最大面積.
如圖∠A=90°,∠B=α,AH=h,α,h為常數,AH⊥BC于H,∠AHE=∠AHD=x,問當x取何值時,△DEH的面積最大?并求出最大面積.查看答案和解析>>
科目:高中數學 來源:2011年高三數學復習(第3章 三角函數與三角恒等變換):3.14 三角最值問題(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com