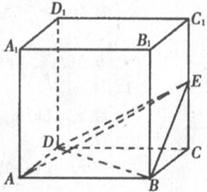
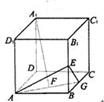
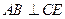已知:正方體
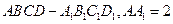
,

為棱
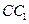
的中點.
(1)求證:
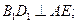
(2)求三棱錐
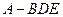
的體積;
(3)求證:
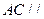
平面
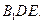
.
(1)證明:連結(jié)
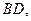
則
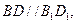
∵

是正方形,
∴
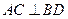
∵
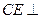
面

∴
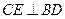
又
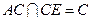
∴
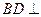
面
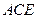
∵
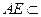
面
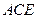
∴
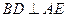
∴

(2)
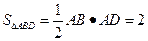
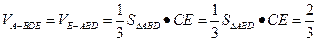
(3)證明:作
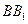
的中點
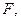
連結(jié)
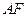
、
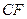
、
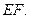
∵

、
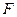
是
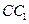
、
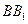
的中點,
∴
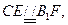
∴四邊形
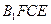
是平行四邊形。
∴
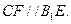
∵
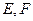
是
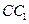
、
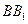
的中點,
∴
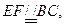
又
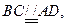
∴
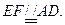
∴四邊形
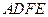
是平行四邊形,
∴
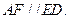
∵
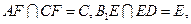
∴平面

面
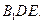
又
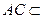
平面
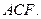
∴
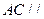
面
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)

(本題14分).如圖所示,在正三棱柱ABC-A
1B
1C
1中,
底面邊長和側(cè)棱長都是2,D是側(cè)棱CC
1上任意一點,E是
A
1B
1的中點.
(1)求證:A
1B
1//平面ABD.
(2)求證:
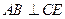
(3)求三棱錐C-ABE的體積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
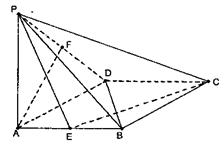
如圖,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F(xiàn)分別是AB與PD的中點.
(1)求證:PC⊥BD;
(2)求證:AF//平面PEC;
(3)求二面角P—EC—D的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在直三棱柱
ABC—
A1B1C1中,
AB=BC=BB1,
D為
AC的中點,
(1)求證:
B1C∥平面
A1BD; (2)若
AC1⊥平面
A1BD,二面角
B—
A1C1—
D的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
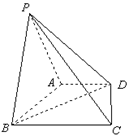
如圖,在四棱錐
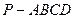
中,底面
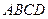
是直角梯形,
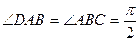
,且
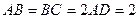
,側(cè)面
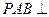
底面
,
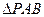
是等邊三角形.
(1)求證:
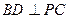
;
(2)求二面角
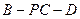
的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖正方體ABCD-
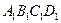
中,E、F、G分別是
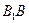
、AB、BC的中點.
(1)證明:
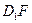
⊥EG;
(2)證明:
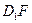
⊥平面AEG;
(3)求
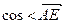
,
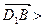
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在正方體
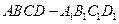
中,
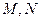
分別是
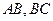
中點.
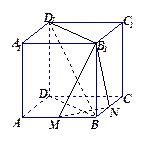
(Ⅰ)求證:平面
⊥平面
;
(Ⅱ)若在棱
上有一點
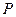
,使
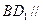
平面
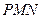
,求
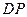
與
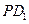
的比.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
一條直線與一個平面垂直,那么,稱此直線與平面構(gòu)成一個“正交線面對”。在一個正方體中,由兩個頂點確定的直線與頂點組成的平面(相同的平面算一個)構(gòu)成的“正交線面對”的個數(shù)是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖所示,在正方體
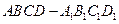
中,
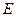
為
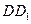
上的點、
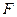
為
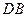
的中點.
(Ⅰ)求直線
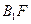
與平面
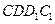
所成角的正弦值;
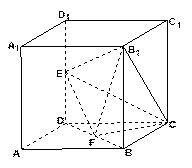
(Ⅱ)若直線
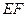
//平面
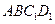
,試確定點
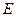
的位置.
查看答案和解析>>

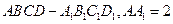 ,
, 為棱
為棱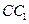 的中點.
的中點.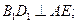
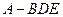 的體積;
的體積;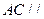 平面
平面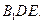 .
.