
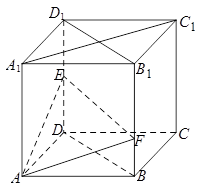
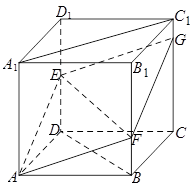
 的正方體
的正方體 中,點
中,點 是棱
是棱 的中點,點
的中點,點 在棱
在棱 上,且滿足
上,且滿足 .
.
 ;
; 上確定一點
上確定一點 ,使
,使 、
、 、
、 、
、 四點共面,并求此時
四點共面,并求此時 的長;
的長; 的體積.
的體積.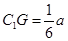 ;(3)
;(3)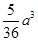 .
.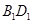 ,先由正方體的性質(zhì)得到
,先由正方體的性質(zhì)得到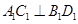 ,以及
,以及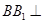 平面
平面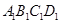 ,從而得到
,從而得到 ,利用直線與平面垂直的判定定理可以得到
,利用直線與平面垂直的判定定理可以得到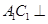 平面
平面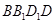 ,于是得到
,于是得到 ;(2)假設(shè)四點
;(2)假設(shè)四點 、
、 、
、 、
、 四點共面,利用平面與平面平行的性質(zhì)定理得到
四點共面,利用平面與平面平行的性質(zhì)定理得到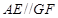 ,
,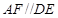 ,于是得到四邊形
,于是得到四邊形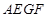 為平行四邊形,從而得到
為平行四邊形,從而得到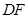 的長度,再結(jié)合勾股定理得到
的長度,再結(jié)合勾股定理得到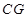 的長度,最終得到
的長度,最終得到 的長度;(3)連接
的長度;(3)連接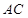 ,由正方體的性質(zhì)得到
,由正方體的性質(zhì)得到 ,結(jié)合(1)中的結(jié)論
,結(jié)合(1)中的結(jié)論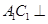 平面
平面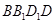 ,得到
,得到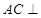 平面
平面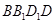 ,然后選擇以點
,然后選擇以點 為頂點,
為頂點,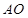 為高,四邊形
為高,四邊形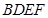 為底面的四棱錐,利用錐體的體積公式計算幾何體
為底面的四棱錐,利用錐體的體積公式計算幾何體 的體積.
的體積.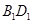 ,
,
 為正方體,所以四邊形
為正方體,所以四邊形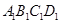 為正方形,所以
為正方形,所以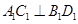 ,
,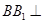 平面
平面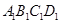 ,
, ,
,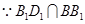 ,
,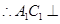 平面
平面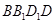 ,
,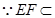 平面
平面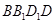 ,
,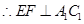 ;
; 、
、 、
、 、
、 四點共面,則
四點共面,則 、
、 、
、 、
、 四點確定平面
四點確定平面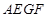 ,
,
 為正方體,所以平面
為正方體,所以平面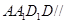 平面
平面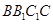 ,
, 平面
平面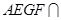 平面
平面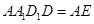 ,平面
,平面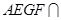 平面
平面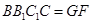 ,
,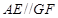 ,
,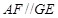 ,因此四邊形
,因此四邊形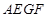 為平行四邊形,
為平行四邊形,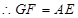 ,
,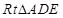 中,
中,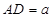 ,
,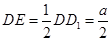 ,
,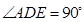 ,
,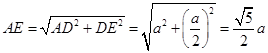 ,
,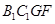 中,下底
中,下底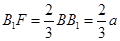 ,直角腰
,直角腰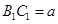 ,斜腰
,斜腰 ,
,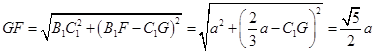 ,
,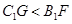 ,解得
,解得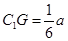 ;
;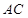 交
交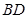 于點
于點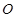 ,
,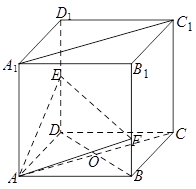
 為正方體,
為正方體,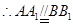 ,
, ,
,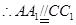 ,
, 為平行四邊形,
為平行四邊形,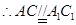 ,
,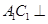 平面
平面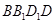 ,所以
,所以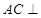 平面
平面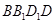 ,
,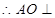 平面
平面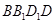 ,
, 為棱長為
為棱長為 正方體,所以
正方體,所以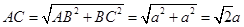 ,
,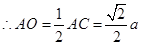 ,
,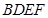 中,直角腰
中,直角腰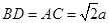 ,上底
,上底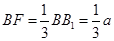 ,下底
,下底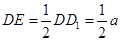 ,
,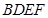 的面積
的面積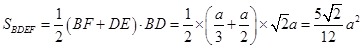 ,
, 的體積
的體積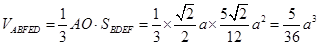 .
.

科目:高中數(shù)學(xué) 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A. π π | B.56π | C.14π | D.64π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A.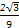 πR3 πR3 | B.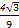 πR3 πR3 |
C.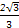 πR3 πR3 | D. πR3 πR3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com