
��D����֪�E�AC��������ԭ�c(di��n)�����c(di��n)��x�S�ϣ��x���ʞ�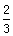 �����^�c(di��n)
�����^�c(di��n)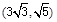 ���c(di��n)A��B�քe�ǙE�AC�L(zh��ng)�S�����Ҷ��c(di��n)���c(di��n)F�ǙE�A���ҽ��c(di��n)���c(di��n)P�ڙE�A�ϣ���λ��
���c(di��n)A��B�քe�ǙE�AC�L(zh��ng)�S�����Ҷ��c(di��n)���c(di��n)F�ǙE�A���ҽ��c(di��n)���c(di��n)P�ڙE�A�ϣ���λ�� �S�Ϸ���
�S�Ϸ���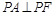 .
.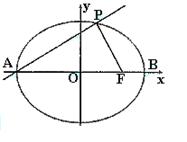
��1����E�AC�ķ��̣�
��2�����c(di��n)P������(bi��o)��
��3���O(sh��)M��ֱ������PAF����ӈA�A�ģ���E�AC�ϵ��c(di��n)���c(di��n)M�ľ��x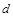 ����Сֵ��
����Сֵ��
��1���E�AC�ķ��̞�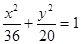 ����2���c(di��n)P������(bi��o)
����2���c(di��n)P������(bi��o)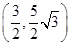 ��
��
��3���E�AC�ϵ��c(di��n)���c(di��n)M�ľ��x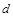 ����Сֵ��
����Сֵ��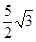 ��
��
����ԇ�}������(1)�O(sh��)�E�A���̞�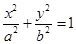 ����
����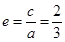 ��
��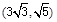 ���뼴�ɽ��
���뼴�ɽ��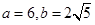 �����E�A���̞�
�����E�A���̞�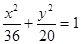 ����2���O(sh��)�c(di��n)P������(bi��o)��
����2���O(sh��)�c(di��n)P������(bi��o)�� ,���
,���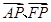 ������(bi��o)������(j��)
������(bi��o)������(j��)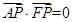 �͙E�A����(li��n)����������c(di��n)P������(bi��o)����3���c(di��n)M������(bi��o)��
�͙E�A����(li��n)����������c(di��n)P������(bi��o)����3���c(di��n)M������(bi��o)��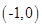 ���Ƀ��c(di��n)֮�g�ľ��x��ʽ��
���Ƀ��c(di��n)֮�g�ľ��x��ʽ��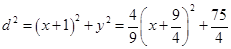 ������
������ ,�ஔ(d��ng)
,�ஔ(d��ng) �r(sh��)��
�r(sh��)��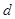 ȡ����Сֵ
ȡ����Сֵ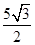 .
.
ԇ�}������(1)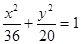 (4��)
(4��)
��2������֪�ɵ��c(di��n)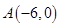 ��
��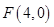
�O(sh��)�c(di��n)P������(bi��o)�� ,�t
,�t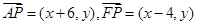 ������֪��
������֪��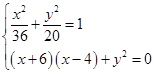 ���t
���t �����
�����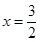 ��
��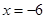 .
.
����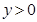 ��ֻ��
��ֻ��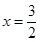 ������
������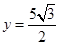 �����c(di��n)
�����c(di��n)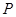 ������(bi��o)��
������(bi��o)��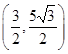 (9�� )
(9�� )
��3�� �c(di��n)M������(bi��o)��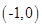 �� �E�A�ϵ��c(di��n)
�� �E�A�ϵ��c(di��n) ���c(di��n)M�ľ��x
���c(di��n)M�ľ��x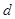 ��
��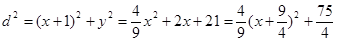
����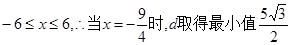 (14��)
(14��)
���c(di��n)���E�A�ķ��̡���ֵ��������(sh��)�c����˼��.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D��ʾ����֪�E�A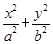 ��1(a��b��0)���ҽ��c(di��n)��F2(1,0)���c(di��n)A
��1(a��b��0)���ҽ��c(di��n)��F2(1,0)���c(di��n)A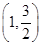 �ڙE�A�ϣ�
�ڙE�A�ϣ�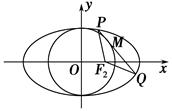
(1)��E�A���̣�
(2)�c(di��n)M(x0��y0)�ڈAx2��y2��b2�ϣ��c(di��n)M�ڵ�һ���ޣ��^�c(di��n)M���Ax2��y2��b2���о����E�A��P��Q���c(di��n)����|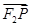 |��|
|��|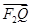 |��|
|��|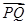 |�Ƿ�鶨ֵ������ǣ����ԓ��ֵ��������ǣ��f�����ɣ�
|�Ƿ�鶨ֵ������ǣ����ԓ��ֵ��������ǣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪��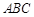 �ăɂ�(g��)��c(di��n)
�ăɂ�(g��)��c(di��n)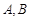 ������(bi��o)�քe��
������(bi��o)�քe��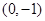 ��
��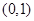 ����
����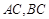 ����ֱ����б��֮�e����
����ֱ����б��֮�e����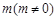 ��
��
��1������c(di��n)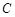 ��܉�E
��܉�E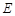 �ķ��̣����Д�܉�E
�ķ��̣����Д�܉�E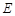 ��ηN�A�F������
��ηN�A�F������
��2����(d��ng)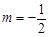 �r(sh��)���^�c(di��n)
�r(sh��)���^�c(di��n)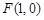 ��ֱ��
��ֱ��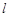 ������
������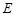 ��
��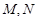 ���c(di��n)���O(sh��)�c(di��n)
���c(di��n)���O(sh��)�c(di��n)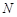 �P(gu��n)��
�P(gu��n)�� �S��(du��)�Q�c(di��n)��
�S��(du��)�Q�c(di��n)��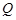 (
(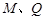 ���غ�)�� ԇ����ֱ��
���غ�)�� ԇ����ֱ�� �c
�c �S�Ľ��c(di��n)�Ƿ��Ƕ��c(di��n)�����ǣ�������c(di��n)�������ǣ�Ո(q��ng)�f������.
�S�Ľ��c(di��n)�Ƿ��Ƕ��c(di��n)�����ǣ�������c(di��n)�������ǣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)�E�A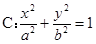
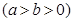 �^�c(di��n)
�^�c(di��n)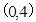 ���x���ʞ�
���x���ʞ�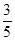 .
.
��1����E�A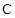 �ķ��̣�
�ķ��̣�
��2�����^�c(di��n)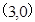 ��б�ʞ�
��б�ʞ�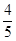 ��ֱ�����E�A���صþ��ε����c(di��n)����(bi��o).
��ֱ�����E�A���صþ��ε����c(di��n)����(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���タ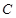 ����c(di��n)������(bi��o)ԭ�c(di��n)
����c(di��n)������(bi��o)ԭ�c(di��n)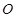 ����(du��)�Q�S��
����(du��)�Q�S��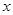 �S�����c(di��n)��
�S�����c(di��n)��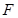 ,���タ��һ�c(di��n)
,���タ��һ�c(di��n) �ęM����(bi��o)��2����
�ęM����(bi��o)��2����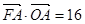 .
.
(1)���タ�ķ��̣�
(2)�^�c(di��n)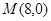 ��ֱ��
��ֱ��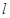 �����タ��
�����タ��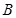 ��
��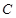 ���c(di��n),���C:
���c(di��n),���C: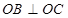 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪?ji��ng)�ֱ��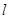 �c�E�A
�c�E�A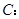
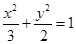 ����
����
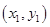 ��
��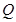
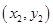 �ɲ�ͬ�c(di��n)���ҡ�
�ɲ�ͬ�c(di��n)���ҡ�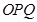 ����e
����e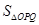 =
=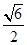 ������
������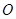 ������(bi��o)ԭ�c(di��n).
������(bi��o)ԭ�c(di��n).
��1���C�� ��
��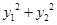 ���鶨ֵ��
���鶨ֵ��
��2���O(sh��)����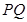 �����c(di��n)��
�����c(di��n)�� ����
����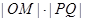 �����ֵ��
�����ֵ��
��3���E�A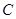 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)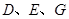 ��ʹ��
��ʹ��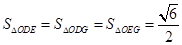 �������ڣ��Д��
�������ڣ��Д�� ���Π�������ڣ�Ո(q��ng)�f������.
���Π�������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A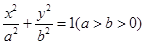 �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��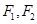 ���x���ʞ�
���x���ʞ�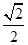 ��P�ǙE�A��һ�c(di��n)����
��P�ǙE�A��һ�c(di��n)����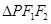 ��e�����ֵ����2��
��e�����ֵ����2��
(1)��E�A�ķ��̣�
(2)ֱ��y=2���Ƿ�����c(di��n)Q��ʹ�Ï�ԓ�c(di��n)��E�A�����ăɗl�о����ֱ�������ڣ����c(di��n)Q������(bi��o)���������ڣ��f�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A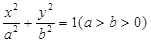 �ϵ��c(di��n)
�ϵ��c(di��n)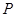 �����҃ɽ��c(di��n)
�����҃ɽ��c(di��n)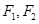 �ľ��x֮�͞�
�ľ��x֮�͞�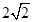 ���x���ʞ�
���x���ʞ�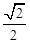 .
.
��1����E�A�ķ��̣�
��2���^�ҽ��c(di��n)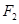 ��ֱ��
��ֱ��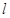 ���E�A��
���E�A��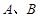 ���c(di��n)����
���c(di��n)����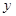 �S��һ�c(di��n)
�S��һ�c(di��n)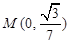 �M��
�M��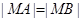 ����ֱ��
����ֱ��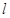 ��б��
��б��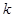 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A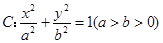 ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)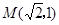 ,�x���ʞ�
,�x���ʞ�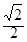 ��
��
(1)��E�AC�ķ��̣�
(2)�^�c(di��n)Q(1,0)��ֱ��l�c�E�AC�ཻ��A��B���c(di��n),�c(di��n)P(4,3),ӛֱ��PA,PB��б�ʷքe��k1,k2,��(d��ng)k1��k2���r(sh��),��ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com