
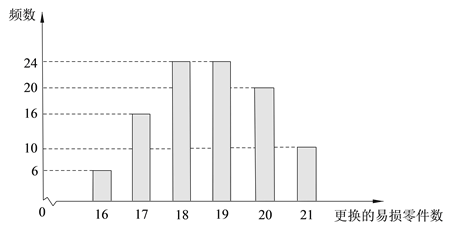
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖:
記x表示1臺機器在三年使用期內需更換的易損零件數,y表示1臺機器在購買易損零件上所需的費用(單位:元), ![]() 表示購機的同時購買的易損零件數.
表示購機的同時購買的易損零件數.
(Ⅰ)若![]() =19,求y與x的函數解析式;
=19,求y與x的函數解析式;
(Ⅱ)若要求“需更換的易損零件數不大于![]() ”的頻率不小于0.5,求
”的頻率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假設這100臺機器在購機的同時每臺都購買19個易損零件,或每臺都購買20個易損零件,分別計算這100臺機器在購買易損零件上所需費用的平均數,以此作為決策依據,購買1臺機器的同時應購買19個還是20個易損零件?
【答案】(1) ![]() ;(2)19;(3) 購買1臺機器的同時應購買19個易損零件.
;(2)19;(3) 購買1臺機器的同時應購買19個易損零件.
【解析】試題分析:(Ⅰ)分x![]() 19及x>19,分別求解析式;(Ⅱ)通過頻率大小進行比較;(Ⅲ)分別求出n=19,n=20時所需費用的平均數來確定.
19及x>19,分別求解析式;(Ⅱ)通過頻率大小進行比較;(Ⅲ)分別求出n=19,n=20時所需費用的平均數來確定.
試題解析:(Ⅰ)當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,所以
,所以![]() 與
與![]() 的函數解析式為
的函數解析式為![]() .
.
(Ⅱ)由柱狀圖知,需更換的零件數不大于18的頻率為0.46,不大于19的頻率為0.7,故![]() 的最小值為19.
的最小值為19.
(Ⅲ)若每臺機器在購機同時都購買19個易損零件,則這100臺機器中有70臺在購買易損零件上的費用為3 800,20臺的費用為4 300,10臺的費用為4 800,因此這100臺機器在購買易損零件上所需費用的平均數為![]() .
.
若每臺機器在購機同時都購買20個易損零件,則這100臺機器中有90臺在購買易損零件上的費用為4 000,10臺的費用為4 500,因此這100臺機器在購買易損零件上所需費用的平均數為![]() .
.
比較兩個平均數可知,購買1臺機器的同時應購買19個易損零件.


科目:高中數學 來源: 題型:
【題目】已知袋子中放有大小和形狀相同的小球若干,其中標號為0的小球1個,標號為1的小球1個,標號為2的小球![]() 個.若從袋子中隨機抽取1個小球,取到標號為2的小球的概率是
個.若從袋子中隨機抽取1個小球,取到標號為2的小球的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)從袋子中不放回地隨機抽取2個小球,記第一次取出的小球標號為![]() ,第二次取出的小球標號為
,第二次取出的小球標號為![]() .求在區間
.求在區間![]() 內任取2個實數
內任取2個實數![]() ,
,![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】研究變量![]() ,
,![]() 得到一組樣本數據,進行回歸分析,有以下結論
得到一組樣本數據,進行回歸分析,有以下結論
①殘差平方和越小的模型,擬合的效果越好;
②用相關指數![]() 來刻畫回歸效果,
來刻畫回歸效果,![]() 越小說明擬合效果越好;
越小說明擬合效果越好;
③線性回歸方程對應的直線![]() 至少經過其樣本數據點中的一個點;
至少經過其樣本數據點中的一個點;
④若變量![]() 和
和![]() 之間的相關系數為
之間的相關系數為![]() ,則變量
,則變量![]() 和
和![]() 之間的負相關很強.
之間的負相關很強.
以上正確說法的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某物流公司引進了一套無人智能配貨系統,購買系統的費用為80萬元,維持系統正常運行的費用包括保養費和維修費兩部分,每年的保養費用為1萬元.該系統的維修費為:第一年![]() 萬元,第二年
萬元,第二年![]() 萬元,第三年2萬元,…,依等差數列逐年遞增.
萬元,第三年2萬元,…,依等差數列逐年遞增.
(1)求該系統使用n年的總費用![]() (包括購買設備的費用);
(包括購買設備的費用);
(2)求該系統使用多少年報廢,使年平均費用最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校在學校內招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者.將這
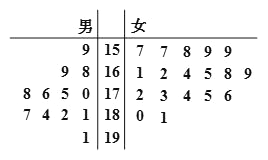
名女志愿者.將這![]() 名志愿者的身高編成如右莖葉圖(單位:
名志愿者的身高編成如右莖葉圖(單位: ![]() ),若身高在
),若身高在![]() 以上(包括
以上(包括![]() )定義為“高個子”,身高在
)定義為“高個子”,身高在![]() 以下(不包括
以下(不包括![]() )定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
)定義為“非高個子”,且只有“女高個子”才能擔任“禮儀小姐”.
(Ⅰ)如果用分層抽樣的方法從“高個子”和“非高個子”中抽取![]() 人,再從這
人,再從這![]() 人中選
人中選![]() 人,那么至少有一人是“高個子”的概率是多少?
人,那么至少有一人是“高個子”的概率是多少?
(Ⅱ)若從所有“高個子”中選![]() 名志愿者,用
名志愿者,用![]() 表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出
表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出![]() 的分布列,并求
的分布列,并求![]() 的數學期望.
的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com