對于0≤m≤4的m,不等式x2+mx>4x+m-3恒成立,則x的取值范圍是 .
【答案】
分析:由對于0≤m≤4的m,不等式x
2+mx>4x+m-3恒成立,可變形為m(x-1)+x
2-4x+3>0在0≤m≤4時恒成立.由于該函數為關于m的一次函數估可轉化為
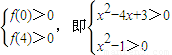
,解不等式組,即可得到結論.
解答:解:若不等式x
2+mx>4x+m-3恒成立
則m(x-1)+x
2-4x+3>0在0≤m≤4時恒成立.
令f(m)=m(x-1)+x
2-4x+3.
則
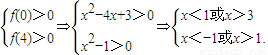
∴x<-1或x>3.
故答案為:x>3或x<-1
點評:解不等式恒成立問題,通常借助于函數思想或方程思想轉化為求函數的最值或利用函數的圖象或判別式的方法求解.

 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案 ABC考王全優卷系列答案
ABC考王全優卷系列答案