
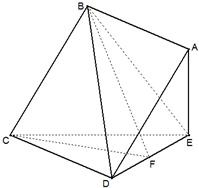
 如圖,在四棱錐E-ABCD中,底面ABCD為正方形,AE⊥平面CDE,已知AE=DE=3,F(xiàn)為線段DE上的動點.
如圖,在四棱錐E-ABCD中,底面ABCD為正方形,AE⊥平面CDE,已知AE=DE=3,F(xiàn)為線段DE上的動點.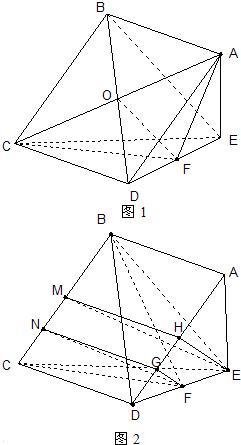 證明:(Ⅰ)連接AC,BD交于O,連OF,如圖1
證明:(Ⅰ)連接AC,BD交于O,連OF,如圖1| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| GF |
| GN |
| 5 |
| 10 |
| 2 |
| DF |
| DE |
| GF |
| EH |
| 5 |
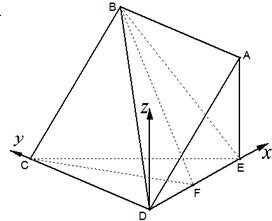 則E(3,0,0),F(xiàn)(a,0,0),C(0,3
則E(3,0,0),F(xiàn)(a,0,0),C(0,3| 2 |
| DC |
| AB |
| 2 |
| n1 |
| n1 |
|
|
| n1 |
| n2 |
| n2 |
|
|
| n2 |
| 2 |
| 2 |
| n3 |
| n3 |
|
|
| n2 |
| 2 |
| 2 |
| n1 |
| n2 |
| n3 |
| n2 |
|
| ||||
|
|
|
| ||||
|
|
| |12+a| | ||
|
| 5 |
| 5 |


 星級口算天天練系列答案
星級口算天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
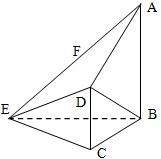 如圖,在四棱錐E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F(xiàn)為AE中點.
如圖,在四棱錐E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F(xiàn)為AE中點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,在四棱錐E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如圖,在四棱錐E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
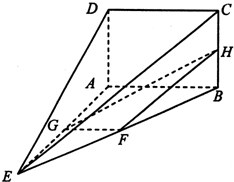 (2013•貴陽二模)如圖,在四棱錐E-ABCD中,矩形ABCD所在的平面與平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F(xiàn),G,H分別為BE,AE,BC的中點
(2013•貴陽二模)如圖,在四棱錐E-ABCD中,矩形ABCD所在的平面與平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F(xiàn),G,H分別為BE,AE,BC的中點| GP |
| GF |
| π |
| 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2012•淮南二模)如圖,在四棱錐E-ABCD中,四邊形ABCD為平行四邊形,BE=BC,AE⊥BE,M為CE上一點,且BM⊥面ACE.
(2012•淮南二模)如圖,在四棱錐E-ABCD中,四邊形ABCD為平行四邊形,BE=BC,AE⊥BE,M為CE上一點,且BM⊥面ACE.| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分) 如圖,在四棱錐E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如圖,在四棱錐E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
AB=BC=CE=2CD=2,∠BCE=1200,F(xiàn)為AE中點。
(Ⅰ) 求證:平面ADE⊥平面ABE ;
(Ⅱ) 求二面角A—EB—D的大小的余弦值;
(Ⅲ)求點F到平面BDE的距離。
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com