
【題目】下列命題:①![]() 使得
使得![]() 成立;②
成立;②![]() ,都有
,都有![]() 成立,是
成立,是![]() 在區間D上單調遞增的充要條件;③只要函數有零點,我們就可以用二分法求出零點的近似值;④過點
在區間D上單調遞增的充要條件;③只要函數有零點,我們就可以用二分法求出零點的近似值;④過點![]() 作直線,使它與拋物線
作直線,使它與拋物線![]() 僅有一個公共點,這樣的直線有2條;正確的個數是( )
僅有一個公共點,這樣的直線有2條;正確的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
對于①,配方法說明![]() 恒成立,則①錯誤;對于②,舉反例
恒成立,則①錯誤;對于②,舉反例![]() ,即可說明②錯誤;對于③,舉反例
,即可說明②錯誤;對于③,舉反例![]() ,說明③錯誤;對于④,求出滿足題意的直線,共有3條,說明④錯誤,從而得解.
,說明③錯誤;對于④,求出滿足題意的直線,共有3條,說明④錯誤,從而得解.
對于①,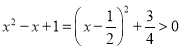 對
對![]() 恒成立,故①錯誤.
恒成立,故①錯誤.
對于②,函數![]() 在
在![]() 上單調遞增,其導數
上單調遞增,其導數![]() ,
,![]() ,此時不滿足“對
,此時不滿足“對![]() ,都有
,都有![]() 成立”,故②錯誤.
成立”,故②錯誤.
對于③,函數![]() 有一個零點
有一個零點![]() ,由于
,由于![]() 恒成立,不存在區間
恒成立,不存在區間![]() 使得
使得![]() ,故無法使用二分法求出零點的近似值,故③錯誤.
,故無法使用二分法求出零點的近似值,故③錯誤.
對于④,當斜率不存在時,直線方程為:![]() ,與拋物線僅有一個公共點,
,與拋物線僅有一個公共點,
當斜率存在時,設直線方程為![]() ,
,
當![]() 時,直線方程為:
時,直線方程為:![]() ,與拋物線只有一個公共點
,與拋物線只有一個公共點![]() ,
,
當![]() 時,聯立直線與拋物線方程,得
時,聯立直線與拋物線方程,得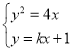 ,
,
消元整理得![]() ,
,
由題可知該方程有兩個相等實根,
即![]() ,解得
,解得![]() ,
,
![]() 直線
直線![]() 與拋物線只有一個公共點,
與拋物線只有一個公共點,
綜上所述,與拋物線![]() 僅有一個公共點的直線有3條,故④錯誤.
僅有一個公共點的直線有3條,故④錯誤.
![]() 正確的個數是
正確的個數是![]() .
.
故選:D.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】天氣預報說,今后三天每天下雨的概率相同,現用隨機模擬的方法預測三天中有兩天下雨的概率,用骰子點數來產生隨機數.依據每天下雨的概率,可規定投一次骰子出現1點和2點代表下雨;投三次骰子代表三天;產生的三個隨機數作為一組.得到的10組隨機數如下:613,265,114,236,561,435,443,251,154,353.則在此次隨機模擬試驗中,每天下雨的概率的近似值是__________,三天中有兩天下雨的概率的近似值為__________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】團購已成為時下商家和顧客均非常青睞的一種省錢、高校的消費方式,不少商家同時加入多家團購網.現恰有三個團購網站在![]() 市開展了團購業務,
市開展了團購業務, ![]() 市某調查公司為調查這三家團購網站在本市的開展情況,從本市已加入了團購網站的商家中隨機地抽取了50家進行調查,他們加入這三家團購網站的情況如下圖所示.
市某調查公司為調查這三家團購網站在本市的開展情況,從本市已加入了團購網站的商家中隨機地抽取了50家進行調查,他們加入這三家團購網站的情況如下圖所示.
(1)從所調查的50家商家中任選兩家,求他們加入團購網站的數量不相等的概率;
(2)從所調查的50家商家中任取兩家,用![]() 表示這兩家商家參加的團購網站數量之差的絕對值,求隨機變量
表示這兩家商家參加的團購網站數量之差的絕對值,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(3)將頻率視為概率,現從![]() 市隨機抽取3家已加入團購網站的商家,記其中恰好加入了兩個團購網站的商家數為
市隨機抽取3家已加入團購網站的商家,記其中恰好加入了兩個團購網站的商家數為![]() ,試求事件“
,試求事件“![]() ”的概率.
”的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]()
![]() 的離心率為
的離心率為![]() ,其右焦點到點
,其右焦點到點![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 不是左右頂點),且以
不是左右頂點),且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 的右頂點,求證直線
的右頂點,求證直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一旅游區有兩個新建項目![]() 、
、![]() .
.![]() 項目的一期投資額
項目的一期投資額![]() 與利潤
與利潤![]() 近似滿足
近似滿足![]() .
.![]() 項目的一期投資額
項目的一期投資額![]() 與利潤
與利潤![]() 的關系如散點圖所示,其中
的關系如散點圖所示,其中![]()
![]() ,
,![]() ,
,![]() .一商家欲向這兩個項目一期隨機投資,其中投資
.一商家欲向這兩個項目一期隨機投資,其中投資![]() 項目不超過10(本題未注明金額單位的,單位均為百萬元).投資
項目不超過10(本題未注明金額單位的,單位均為百萬元).投資![]() 、
、![]() 相互獨立.
相互獨立.
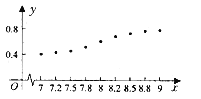
(1)用最小二乘法求![]() 與
與![]() 的回歸直線方程;
的回歸直線方程;
(2)商家投資![]() 項目的概率是0.4,投資
項目的概率是0.4,投資![]() 項目的概率是0.6.設商家這次投資獲得的利潤最大值為
項目的概率是0.6.設商家這次投資獲得的利潤最大值為![]() ,利用(1)的結果,求
,利用(1)的結果,求![]() .
.
附參考公式: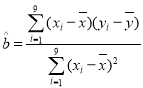 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本小題滿分13分)
工作人員需進入核電站完成某項具有高輻射危險的任務,每次只派一個人進去,且每個人只派一次,工作時間不超過10分鐘,如果有一個人10分鐘內不能完成任務則撤出,再派下一個人.現在一共只有甲、乙、丙三個人可派,他們各自能完成任務的概率分別![]()
![]() ,假設
,假設![]() 互不相等,且假定各人能否完成任務的事件相互獨立.
互不相等,且假定各人能否完成任務的事件相互獨立.
(1)如果按甲在先,乙次之,丙最后的順序派人,求任務能被完成的概率.若改變三個人被派出的先后順序,任務能被完成的概率是否發生變化?
(2)若按某指定順序派人,這三個人各自能完成任務的概率依次為![]() ,其中
,其中![]() 是
是![]() 的一個排列,求所需派出人員數目
的一個排列,求所需派出人員數目![]() 的分布列和均值(數字期望)
的分布列和均值(數字期望)![]() ;
;
(3)假定![]() ,試分析以怎樣的先后順序派出人員,可使所需派出的人員數目的均值(數字期望)達到最小.
,試分析以怎樣的先后順序派出人員,可使所需派出的人員數目的均值(數字期望)達到最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若點![]() 為點
為點![]() 在平面
在平面![]() 上的正投影,則記
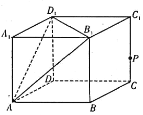
上的正投影,則記![]() .如圖,在棱長為1的正方體
.如圖,在棱長為1的正方體![]() 中,記平面
中,記平面![]() 為
為![]() ,平面
,平面![]() 為
為![]() ,點
,點![]() 是線段
是線段![]() 上一動點,
上一動點,![]() .給出下列四個結論:
.給出下列四個結論:
①![]() 為
為![]() 的重心;
的重心;
②![]() ;
;
③當![]() 時,
時,![]() 平面
平面![]() ;
;
④當三棱錐![]() 的體積最大時,三棱錐
的體積最大時,三棱錐![]() 外接球的表面積為
外接球的表面積為![]() .
.
其中,所有正確結論的序號是________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com