三级国产网站,国产不卡免费视频,亚洲视频免费网站

精英家教網 > 高中數學 > 題目詳情

【題目】設F1和F2為雙曲線 ﹣ =1（a＞0，b＞0）的兩個焦點，若F1 ， F2 ， P（0，2b）是正三角形的三個頂點，則雙曲線的漸近線方程是（　　）
A.y=± x
B.y=± x
C.y=± x
D.y=± x

【答案】B
【解析】解：若F1，F2，P（0，2b）是正三角形的三個頂點，

設F1（﹣c，0），F2（c，0），則|F1P|= ，

∵F1、F2、P（0，2b）是正三角形的三個頂點，

∴ =2c，∴c2+4b2=4c2，

∴c2+4（c2﹣a2）=4c2，

∴c2=4a2，即c=2a，

b= = a，

∴雙曲線的漸近線方程為y=± x，

即為y=± x．

故答案為：B．

根據F1，F2，P（0，2b）是正三角形的三個頂點，求得c與b的關系式，再結合雙曲線中a，b，c三者的關系，即可求得雙曲線的漸近線的方程.

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】函數f（x）=sin（2x+φ），其中φ為實數，若f（x）≤|f（）|對（0，+∞）恒成立，且，則f（x）的單調遞增區間是．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=ln（x+1）﹣x2+（2﹣a）x﹣a（a∈R）若存在唯一的正整數x0 ，使得f（x0）＞0，則實數a的取值范圍是（　　）
A.[ ， ]
B.（，）
C.（， ]
D.（ln3，ln2+1）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】設全集U=R，集合M={x|x2+x﹣2＞0}，，則（UM）∩N=（　　）
A.[﹣2，0]
B.[﹣2，1]
C.[0，1]
D.[0，2]

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖所示的多面體是由一個直平行六面體被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．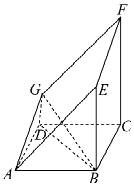

（1）求證：BD⊥平面ADG；
（2）求直線GB與平面AEFG所成角的正弦值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=2cos2x+2 sinxcosx+a，且當x∈[0， ]時，f（x）的最小值為2．
（Ⅰ）求a 的值；
（Ⅱ）先將函數y=f （x）的圖象上點的縱坐標不變，橫坐標縮小為原來的，再將所得的圖象向右平移個單位，得到函數y=g（x）的圖象，求方程g（x）=4在區間[0， ]上所有根之和．