如果函數y=f(x)圖象上任意一點的坐標(x,y)都滿足方程 lg(x+y)=lgx+lgy,那么正確的選項是( )
A.y=f(x)是區間(0,+∞)上的減函數,且x+y≤4
B.y=f(x)是區間(1,+∞)上的增函數,且x+y≥4
C.y=f(x)是區間(1,+∞)上的減函數,且x+y≥4
D.y=f(x)是區間(1,+∞)上的減函數,且x+y≤4
【答案】
分析:由給出的方程得到函數y=f(x)圖象上任意一點的橫縱坐標x,y的關系式,利用基本不等式求出x+y的范圍,利用函數單調性的定義證明函數在(1,+∞)上的增減性,二者結合可得正確答案.
解答:解:由lg(x+y)=lgx+lgy,得

,
由x+y=xy得:
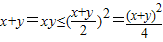
,
解得:x+y≥4.
再由x+y=xy得:
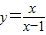
(x≠1).
設x
1>x
2>1,
則
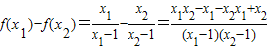
=
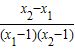
.
因為x
1>x
2>1,
所以x
2-x
10,x
2-1>0.
則
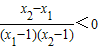
,即f(x
1)<f(x
2).
所以y=f(x)是區間(1,+∞)上的減函數,
綜上,y=f(x)是區間(1,+∞)上的減函數,且x+y≥4.
故選C.
點評:本題考查了函數單調性的判斷與證明,考查了利用基本不等式求最值,訓練了利用單調性定義證明函數單調性的方法,是基礎題.

 ,
,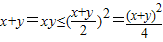 ,
,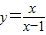 (x≠1).
(x≠1).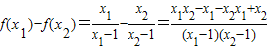 =
=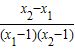 .
.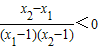 ,即f(x1)<f(x2).
,即f(x1)<f(x2).
