數列{an}滿足Sn=2n-an,n∈N+.(Sn為前n項和)
(1)計算a1,a2,a3,a4,并由此猜想an;(2)用數學歸納法證明(1)中的結論.
【答案】
分析:(1)由題意S
n=2S
n=2n-a
n,令n=1因為s
1=a
1,可求出a
1的值,再反復代入S
n=2n-a
n,分別求出a
2,a
3,a
4,總結出規(guī)律;
(2)根據(1)的猜想,利用歸納法進行證明,假設n=k成立,然后利用已知條件驗證n=k+1是否成立,從而求證.
解答:解:(1)a
1=s
1=2-a
1,∴a
1=1,
s
2=a
1+a
2=2×2-a
2,
∴a
2=

,s
3=a
1+a
2+a
3=2×3-a
3,
∴a
3=

,
s
4-s
3=a
4,
∴2×4-a
4-a
3=a
4,a
4=
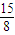
,
猜想a
n=2-
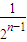
(n∈N
+).
(2)證明:①當n=1時,a
1=2-
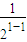
=1-1=1,猜想結論成立.
②假設當n=k(k≥1)時結論成立,即a
k=2-
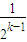
.
當n=k+1時a
k+1=s
k+1-s
k=2(k+1)-a
k+1-2k+a
k,
2a
k+1=2+a
k,a
k+1=1+
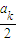
=1+1-
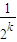
=2-
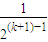
.
所以當n=k+1時,猜想結論成立.
由(1)和(2)可知,對一切n(n∈N
+)結論成立.
點評:此題主要考查數列的遞推公式和利用數學歸納法進行證明,歸納法是高考中常考的方法,幾乎每年都考,對此學生要引起注意,多加練習.

 ,s3=a1+a2+a3=2×3-a3,
,s3=a1+a2+a3=2×3-a3, ,
,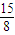 ,
,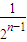 (n∈N+).
(n∈N+).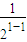 =1-1=1,猜想結論成立.
=1-1=1,猜想結論成立.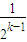 .
.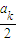 =1+1-
=1+1-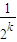 =2-
=2-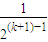 .
.
