
【題目】已知函數f(x)=ax2﹣x﹣lnx,a∈R.
(1)當 ![]() 時,求函數f(x)的最小值;
時,求函數f(x)的最小值;
(2)若﹣1≤a≤0,證明:函數f(x)有且只有一個零點;
(3)若函數f(x)有兩個零點,求實數a的取值范圍.
【答案】
(1)解:當 ![]() 時,
時, ![]() .
.
所以 ![]() ,(x>0).
,(x>0).
令f'(x)=0,得x=2,
當x∈(0,2)時,f'(x)<0;當x∈(2,+∞)時,f'(x)>0,
所以函數f(x)在(0,2)上單調遞減,在(2,+∞)上單調遞增.
所以當x=2時,f(x)有最小值 ![]()
(2)解:由f(x)=ax2﹣x﹣lnx,得 ![]() .
.
所以當a≤0時, ![]() ,
,
函數f(x)在(0,+∞)上單調遞減,
所以當a≤0時,函數f(x)在(0,+∞)上最多有一個零點
因為當﹣1≤a≤0時,f(1)=a﹣1<0, ![]() ,
,
所以當﹣1≤a≤0時,函數f(x)在(0,+∞)上有零點.
綜上,當﹣1≤a≤0時,函數f(x)有且只有一個零點
(3)解:由(2)知,當a≤0時,函數f(x)在(0,+∞)上最多有一個零點.
因為函數f(x)有兩個零點,所以a>0.
由f(x)=ax2﹣x﹣lnx,得 ![]() ,令g(x)=2ax2﹣x﹣1.
,令g(x)=2ax2﹣x﹣1.
因為g(0)=﹣1<0,2a>0,
所以函數g(x)在(0,+∞)上只有一個零點,設為x0.
當x∈(0,x0)時,g(x)<0,f'(x)<0;當x∈(x0,+∞)時,g(x)>0,f'(x)>0.
所以函數f(x)在(0,x0)上單調遞減;在(x0,+∞)上單調遞增.
要使得函數f(x)在(0,+∞)上有兩個零點,
只需要函數f(x)的極小值f(x0)<0,即 ![]() .
.
又因為 ![]() ,所以2lnx0+x0﹣1>0,
,所以2lnx0+x0﹣1>0,
又因為函數h(x)=2lnx+x﹣1在(0,+∞)上是增函數,且h(1)=0,
所以x0>1,得 ![]() .
.
又由 ![]() ,得
,得 ![]() ,
,
所以0<a<1. …13分
以下驗證當0<a<1時,函數f(x)有兩個零點.
當0<a<1時, ![]() ,
,
所以 ![]() .
.
因為 ![]() ,且f(x0)<0.
,且f(x0)<0.
所以函數f(x)在 ![]() 上有一個零點.
上有一個零點.
又因為 ![]() (因為lnx≤x﹣1),且f(x0)<0.
(因為lnx≤x﹣1),且f(x0)<0.
所以函數f(x)在 ![]() 上有一個零點.
上有一個零點.
所以當0<a<1時,函數f(x)在 ![]() 內有兩個零點.
內有兩個零點.
綜上,實數a的取值范圍為(0,1).
下面證明:lnx≤x﹣1.
設t(x)=x﹣1﹣lnx,所以 ![]() ,(x>0).
,(x>0).
令t'(x)=0,得x=1.
當x∈(0,1)時,t'(x)<0;當x∈(1,+∞)時,t'(x)>0.
所以函數t(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增.
所以當x=1時,t(x)有最小值t(1)=0.
所以t(x)=x﹣1﹣lnx≥0,得lnx≤x﹣1成立
【解析】(1)當 ![]() 時,
時, ![]() .求出函數的導數,得到極值點,然后判斷單調性求解函數的最值.(2)由f(x)=ax2﹣x﹣lnx,得
.求出函數的導數,得到極值點,然后判斷單調性求解函數的最值.(2)由f(x)=ax2﹣x﹣lnx,得 ![]() .當a≤0時,函數f(x)在(0,+∞)上最多有一個零點,當﹣1≤a≤0時,f(1)=a﹣1<0,
.當a≤0時,函數f(x)在(0,+∞)上最多有一個零點,當﹣1≤a≤0時,f(1)=a﹣1<0, ![]() ,推出結果.(3)由(2)知,當a≤0時,函數f(x)在(0,+∞)上最多有一個零點.說明a>0,由f(x)=ax2﹣x﹣lnx,得
,推出結果.(3)由(2)知,當a≤0時,函數f(x)在(0,+∞)上最多有一個零點.說明a>0,由f(x)=ax2﹣x﹣lnx,得 ![]() ,說明函數f(x)在(0,x0)上單調遞減;在(x0 , +∞)上單調遞增. 要使得函數f(x)在(0,+∞)上有兩個零點,只需要
,說明函數f(x)在(0,x0)上單調遞減;在(x0 , +∞)上單調遞增. 要使得函數f(x)在(0,+∞)上有兩個零點,只需要 ![]() .通過函數h(x)=2lnx+x﹣1在(0,+∞)上是增函數,推出0<a<1.驗證當0<a<1時,函數f(x)有兩個零點.證明:lnx≤x﹣1.
.通過函數h(x)=2lnx+x﹣1在(0,+∞)上是增函數,推出0<a<1.驗證當0<a<1時,函數f(x)有兩個零點.證明:lnx≤x﹣1.
設t(x)=x﹣1﹣lnx,利用導數求解函數的最值即可.
【考點精析】認真審題,首先需要了解函數的極值與導數(求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值).
是極小值).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】我國古代數學著作《九章算術》中有這樣一個題目:“今有蒲生一日,長三尺;莞生一日,長一尺.蒲生日自半,莞生日自倍.問幾何日而長等?”.其大意是“今有蒲生長1日,長為3尺;莞生長1日,長為1尺.蒲的生長逐日減其一半,莞的生長逐日增加一倍.問幾日蒲、莞長度相等?”若本題改為求當蒲、莞長度相等時,莞的長度為( )
A. 4尺B. 5尺C. 6尺D. 7尺
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() ,圓Q:x2+y2﹣4x﹣2y+3=0的圓心Q在橢圓C上,點P(0,1)到橢圓C的右焦點的距離為2.
,圓Q:x2+y2﹣4x﹣2y+3=0的圓心Q在橢圓C上,點P(0,1)到橢圓C的右焦點的距離為2. 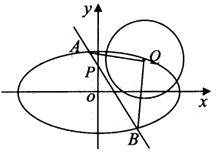
(1)求橢圓C的方程;
(2)過點P作直線l交橢圓C于A,B兩點,若S△AQB=tan∠AQB,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高一某班級在學校數學嘉年華活動中推出了一款數學游戲,受到大家的一致追捧.游戲規則如下:游戲參與者連續拋擲一顆質地均勻的骰子,記第i次得到的點數為![]() ,若存在正整數n,使得
,若存在正整數n,使得![]() ,則稱為游戲參與者的幸運數字。
,則稱為游戲參與者的幸運數字。
(I)求游戲參與者的幸運數字為1的概率;
(Ⅱ)求游戲參與者的幸運數字為2的概率,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將圓的一組![]() 等分點分別涂上紅色或藍色,從任意一點開始,按逆時針方向依次記錄
等分點分別涂上紅色或藍色,從任意一點開始,按逆時針方向依次記錄![]() 個點的顏色,稱為該圓的一個“
個點的顏色,稱為該圓的一個“![]() 階色序”,當且僅當兩個“
階色序”,當且僅當兩個“![]() 階色序”對應位置上的顏色至少有一個不相同時,稱為不同的“
階色序”對應位置上的顏色至少有一個不相同時,稱為不同的“![]() 階色序”.若某圓的任意兩個“
階色序”.若某圓的任意兩個“![]() 階色序”均不相同,則稱該圓為“
階色序”均不相同,則稱該圓為“![]() 階魅力圓”.“4階魅力圓”中最多可有的等分點個數為__________.
階魅力圓”.“4階魅力圓”中最多可有的等分點個數為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 平面上,將兩個半圓弧
平面上,將兩個半圓弧![]() 和
和![]() 、兩條直線
、兩條直線![]() 和
和![]() 圍成的封閉圖形記為
圍成的封閉圖形記為![]() ,如圖中陰影部分.記
,如圖中陰影部分.記![]() 繞
繞![]() 軸旋轉一周而成的幾何體為
軸旋轉一周而成的幾何體為![]() ,過
,過![]() 作
作![]() 的水平截面,所得截面面積為
的水平截面,所得截面面積為![]() ,試利用祖暅原理(祖暅原理:“冪勢既同,則積不容異”,意思是:兩等高的幾何體在同高處被截得的兩個截面面積均相等,那么這兩個幾何體的體積相等)、一個平放的圓柱和一個長方體,得出
,試利用祖暅原理(祖暅原理:“冪勢既同,則積不容異”,意思是:兩等高的幾何體在同高處被截得的兩個截面面積均相等,那么這兩個幾何體的體積相等)、一個平放的圓柱和一個長方體,得出![]() 的體積值為__________.
的體積值為__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}前n項和Sn滿足:2Sn+an=1.
(1)求數列{an}的通項公式;
(2)設 ![]() ,數列{bn}的前n項和為Tn , 求證:Tn<2.
,數列{bn}的前n項和為Tn , 求證:Tn<2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自2016年1月1日起,我國全面二孩政策正式實施,這次人口與生育政策的歷史性調整,使得“要不要再生一個”“生二孩能休多久產假”等成為千千萬萬個家庭在生育決策上避不開的話題.為了解針對產假的不同安排方案形成的生育意愿,某調查機構隨機抽取了200戶有生育二胎能力的適齡家庭進行問卷調查,得到如下數據:
產假安排(單位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭數 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中數據所得的頻率代替概率,面對產假為14周與16周,估計某家庭有生育意愿的概率分別為多少?
(2)假設從5種不同安排方案中,隨機抽取2種不同安排分別作為備選方案,然后由單位根據單位情況自主選擇. ①求兩種安排方案休假周數和不低于32周的概率;
②如果用ξ表示兩種方案休假周數和.求隨機變量ξ的分布及期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com