
【題目】
如圖,已知![]() 是以
是以![]() 的直角三角形鐵皮,
的直角三角形鐵皮,![]() 米,
米,![]() 分別是邊
分別是邊![]() 上不與端點重合的動點,且
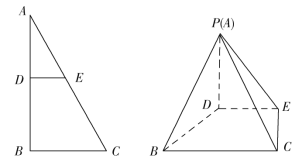
上不與端點重合的動點,且![]() .現將
.現將![]() 鐵皮沿
鐵皮沿![]() 折起至
折起至![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖所示.現要制作一個四棱錐
,如圖所示.現要制作一個四棱錐![]() 的封閉容器,其中
的封閉容器,其中![]() 鐵皮和直角梯形
鐵皮和直角梯形![]() 鐵皮分別是這個封閉容器的一個側面和底面,其他三個側面用相同材料的鐵皮無縫焊接密封而成(假設制作過程中不浪費材料,且鐵皮厚度忽略不計).
鐵皮分別是這個封閉容器的一個側面和底面,其他三個側面用相同材料的鐵皮無縫焊接密封而成(假設制作過程中不浪費材料,且鐵皮厚度忽略不計).
(1)若![]() 為
為![]() 邊的中點,求制作三個新增側面的鐵皮面積是多少平方米?
邊的中點,求制作三個新增側面的鐵皮面積是多少平方米?
(2)求這個封閉容器的最大體積.
科目:高中數學 來源: 題型:
【題目】如圖,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 與焦點在
與焦點在![]() 軸上的橢圓
軸上的橢圓![]() 都過點
都過點![]() ,中心都在坐標原點,且橢圓
,中心都在坐標原點,且橢圓![]() 與
與![]() 的離心率均為
的離心率均為![]() .
.
(Ⅰ)求橢圓![]() 與橢圓
與橢圓![]() 的標準方程;
的標準方程;
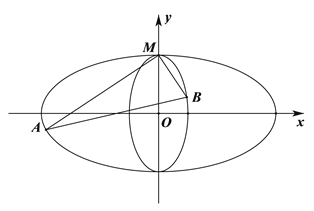
(Ⅱ)過點M的互相垂直的兩直線分別與![]() ,
,![]() 交于點A,B(點A、B不同于點M),當
交于點A,B(點A、B不同于點M),當![]() 的面積取最大值時,求兩直線MA,MB斜率的比值.
的面積取最大值時,求兩直線MA,MB斜率的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點P在曲線y=x2上,從原點向A(2,4)移動,如果直線OP,曲線y=x2及直線x=2所圍成的面積分別記為S1、S2.
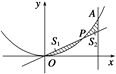
(1)當S1=S2時,求點P的坐標;
(2)當S1+S2有最小值時,求點P的坐標和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知袋子中放有大小和形狀相同標號分別是0,1,2的小球若干,其中標號為0的小球1個,標號為1的小球2個,標號為2的小球n個.若從袋子中隨機抽取1個小球,取到標號為2的小球的概率是![]() .
.
(1)求n的值
(2)從袋子中不放回地隨機抽取2個小球,記第一次取出的小球標號為a,第二次取出的球標號為b.
①記“![]() ”為事件A,求事件A的概率;
”為事件A,求事件A的概率;
②在區間![]() 內任取2個實數x,y,求事件“
內任取2個實數x,y,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有六名同學參加演講比賽,編號分別為1,2,3,4,5,6,比賽結果設特等獎一名,![]() ,
,![]() ,
,![]() ,
,![]() 四名同學對于誰獲得特等獎進行預測.
四名同學對于誰獲得特等獎進行預測.![]() 說:不是1號就是2號獲得特等獎;
說:不是1號就是2號獲得特等獎;![]() 說:3號不可能獲得特等獎;
說:3號不可能獲得特等獎;![]() 說:4,5,6號不可能獲得特等獎;
說:4,5,6號不可能獲得特等獎;![]() 說:能獲得特等獎的是4,5,6號中的一個.公布的比賽結果表明,
說:能獲得特等獎的是4,5,6號中的一個.公布的比賽結果表明,![]() ,
,![]() ,
,![]() ,
,![]() 中只有一個判斷正確.根據以上信息,獲得特等獎的是( )號同學.
中只有一個判斷正確.根據以上信息,獲得特等獎的是( )號同學.
A.1B.2C.3D.4,5,6號中的一個
查看答案和解析>>
科目:高中數學 來源: 題型:
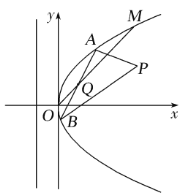
【題目】如圖所示,在直角坐標系![]() 中,點
中,點![]() 到拋物線
到拋物線![]() :
:![]() 的準線的距離為
的準線的距離為![]() .點
.點![]() 是
是![]() 上的定點,
上的定點,![]() ,
,![]() 是
是![]() 上的兩動點,且線段
上的兩動點,且線段![]() 的中點
的中點![]() 在直線
在直線![]() 上.
上.
(1)求曲線![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(2)記![]() ,求弦長
,求弦長![]() (用
(用![]() 表示);并求
表示);并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應國家號召,某校組織部分學生參與了“垃圾分類,從我做起”的知識問卷作答,并將學生的作答結果分為“合格”與“不合格”兩類與“問卷的結果”有關?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握認為“性別”與“問卷的結果”有關?
(2)在成績合格的學生中,利用性別進行分層抽樣,共選取9人進行座談,再從這9人中隨機抽取5人發送獎品,記拿到獎品的男生人數為X,求X的分布列及數學期望![]() .
.
附: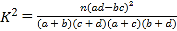
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年10月5日, 美國NBA火箭隊總經理莫雷公開發布涉港錯誤言論,中國公司與明星紛紛站出來抵制火箭隊,隨后京東、天貓、淘寶等中國電商平臺全線下架了火箭隊的所有商品,當天有大量網友關注此事,某網上論壇從關注此事跟帖中,隨機抽取了100名網友進行調查統計,先分別統計他們在跟帖中的留言條數,再把網友人數按留言條數分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
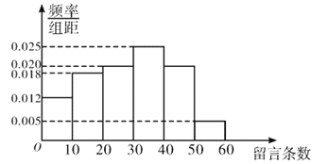
,![]() ,得到如圖所示的頻率分布直方圖;并將其中留言不低于40條的規定為“強烈關注”,否則為“一般關注”,對這100名網友進一步統計得到列聯表的部分數據如下表:
,得到如圖所示的頻率分布直方圖;并將其中留言不低于40條的規定為“強烈關注”,否則為“一般關注”,對這100名網友進一步統計得到列聯表的部分數據如下表:
一般關注 | 強烈關注 | 合計 | |
男 | 60 | ||
女 | 5 | 40 | |
合計 | 100 |
(1)補全列聯表中數據,并判斷能否有![]() 的把握認為網友對此事件是否為“強烈關注”與性別有關?
的把握認為網友對此事件是否為“強烈關注”與性別有關?
(2)現已從男性網友中分層抽樣選取了6人,再從這6人中隨機選取2人,求這2人中至少有1人屬于“強烈關注”的概率.
附: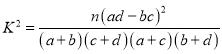 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
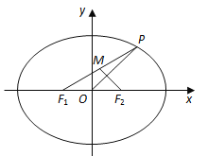
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)若![]() ,點
,點![]() 的坐標為
的坐標為![]() ,求橢圓
,求橢圓![]() 的方程;
的方程;
(2)若點![]() 橫坐標為
橫坐標為![]() ,點
,點![]() 為
為![]() 中點,且
中點,且![]() ,求橢圓
,求橢圓![]() 的離心率.
的離心率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com