
【題目】某城市一社區接到有關部門的通知,對本社區居民用水量進行調研,通過抽樣調查的方法獲得了100戶居民某年的月均用水量(單位:t),通過分組整理數據,得到數據的頻率分布直方圖如圖所示:
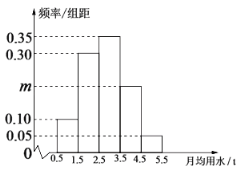
(Ⅰ)求圖中m的值;并估計該社區居民月均用水量的中位數和平均值.(保留3位小數)
(Ⅱ)用此樣本頻率估計概率,若從該社區隨機抽查3戶居民的月均用水量,問恰有2戶超過![]() 的概率為多少?
的概率為多少?
(Ⅲ)若按月均用水量![]() 和
和![]() 分成兩個區間用戶,按分層抽樣的方法抽取10戶,每戶出一人參加水價調整方案聽證會.并從這10人中隨機選取3人在會上進行陳述發言,設來自用水量在區間
分成兩個區間用戶,按分層抽樣的方法抽取10戶,每戶出一人參加水價調整方案聽證會.并從這10人中隨機選取3人在會上進行陳述發言,設來自用水量在區間![]() 的人數為X,求X的分布列和數學期望.
的人數為X,求X的分布列和數學期望.
【答案】(Ⅰ)![]() ,2.786,2.800;(Ⅱ)0.432;(Ⅲ)分布列見解析,
,2.786,2.800;(Ⅱ)0.432;(Ⅲ)分布列見解析,![]()
【解析】
(Ⅰ)根據頻率分布直方圖各小矩形面積和為1,即可求得m的值;根據頻率分布直方圖各小組的頻率,由中位數定義即可求解;結合平均數的求法,可用頻率分布直方圖求得平均數.
(Ⅱ)先求得月均用水量超過![]() 的概率,再結合獨立重復試驗中概率求法即可得恰有2戶超過
的概率,再結合獨立重復試驗中概率求法即可得恰有2戶超過![]() 的概率.
的概率.
(Ⅲ)按照分層抽樣,先求得在月均用水量![]() 和
和![]() 在兩個區間各自抽取的人數,可知來自用水量在區間
在兩個區間各自抽取的人數,可知來自用水量在區間![]() 的人數為X的取值有0,1,2,3,分別求得各自對應的概率即可得分布列,由分布列求得數學期望即可.
的人數為X的取值有0,1,2,3,分別求得各自對應的概率即可得分布列,由分布列求得數學期望即可.
(Ⅰ)由頻率分布直方圖得:
![]() ,
,
解得![]() ,
,
![]() 的頻率為
的頻率為![]() ,
,![]() 的頻率為0.35,
的頻率為0.35,
∴估計該社區居民月均用水量的中位數為:![]()
平均值為:![]() .
.
(Ⅱ)用此樣本頻率估計概率,從該社區隨機抽查3戶居民的月均用水量,
月均用水量超過![]() 的概率為:
的概率為:![]() ,
,
∴恰有2戶超過![]() 的概率為
的概率為![]() .
.
(Ⅲ)若按月均用水量![]() 和
和![]() 分成兩個區間用戶,按分層抽樣的方法抽取10戶,
分成兩個區間用戶,按分層抽樣的方法抽取10戶,
月均用水量![]() 中抽取:
中抽取:![]() 戶,
戶,
月均用水量![]() 中抽取:
中抽取:![]() 戶.
戶.
從這10人中隨機選取3人在會上進行陳述發言,設來自用水量在區間![]() 的人數為X,
的人數為X,
則X的可能取值為0,1,2,3,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴X的分布列為:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
數學期望![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 和
和![]() ,過拋物線
,過拋物線![]() 上一點
上一點![]() 作兩條直線與
作兩條直線與![]() 分別相切于
分別相切于![]() 兩點,分別交拋物線于
兩點,分別交拋物線于![]() 兩點.
兩點.

(1)當![]() 的角平分線垂直
的角平分線垂直![]() 軸時,求直線
軸時,求直線![]() 的斜率;
的斜率;
(2)若直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1852年,英國來華傳教士偉烈亞力將《孫子算經》中“物不知數”問題的解法傳至歐洲.1874年,英國數學家馬西森指出此法符合1801年由高斯得到的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.“中國剩余定理”講的是一個關于整除的問題,例如求1到2000這2000個整數中,能被3除余1且被7除余1的數的個數,現由程序框圖,其中MOD函數是一個求余函數,記![]() 表示m除以n的余數,例如
表示m除以n的余數,例如![]() ,則輸出i為( ).
,則輸出i為( ).
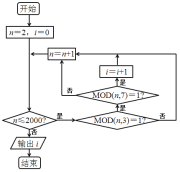
A.98B.97C.96D.95
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (α為參數).以坐標原點O為極點,x軸正半軸為極軸的坐標系中,曲線C2的方程為
(α為參數).以坐標原點O為極點,x軸正半軸為極軸的坐標系中,曲線C2的方程為![]() (m為常數)
(m為常數)
(1)求曲線C1,C2的直角坐標方程;
(2)若曲線C1,C2有兩個交點P、Q,當|PQ|![]() 時,求m的值.
時,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,拋物線
,拋物線![]() 與圓
與圓![]() 的相交弦長為4.
的相交弦長為4.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)點![]() 為拋物線
為拋物線![]() 的焦點,
的焦點,![]() 為拋物線
為拋物線![]() 上兩點,
上兩點,![]() ,若
,若![]() 的面積為
的面積為![]() ,且直線
,且直線![]() 的斜率存在,求直線
的斜率存在,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人設計一項單人游戲,規則如下:先將一棋子放在如圖所示正方形![]() (邊長為2個單位)的頂點
(邊長為2個單位)的頂點![]() 處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數為
處,然后通過擲骰子來確定棋子沿正方形的邊按逆時針方向行走的單位,如果擲出的點數為![]() ,則棋子就按逆時針方向行走
,則棋子就按逆時針方向行走![]() 個單位,一直循環下去.則某人拋擲三次骰子后棋子恰好又回到點
個單位,一直循環下去.則某人拋擲三次骰子后棋子恰好又回到點![]() 處的所有不同走法共有( )
處的所有不同走法共有( )

A. 22種 B. 24種 C. 25種 D. 27種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com