
【題目】如圖,![]() 是底面邊長為1的正三棱錐,
是底面邊長為1的正三棱錐,![]() 分別為棱長
分別為棱長![]() 上的點,截面
上的點,截面![]() 底面
底面![]() ,且棱臺
,且棱臺![]() 與棱錐
與棱錐![]() 的棱長和相等.(棱長和是指多面體中所有棱的長度之和)
的棱長和相等.(棱長和是指多面體中所有棱的長度之和)

(1)證明:![]() 為正四面體;
為正四面體;
(2)若![]() ,求二面角
,求二面角![]() 的大小;(結果用反三角函數值表示)
的大小;(結果用反三角函數值表示)
(3)設棱臺![]() 的體積為
的體積為![]() ,是否存在體積為
,是否存在體積為![]() 且各棱長均相等的直平行六面體,使得它與棱臺
且各棱長均相等的直平行六面體,使得它與棱臺![]() 有相同的棱長和?若存在,請具體構造出這樣的一個直平行六面體,并給出證明;若不存在,請說明理由.
有相同的棱長和?若存在,請具體構造出這樣的一個直平行六面體,并給出證明;若不存在,請說明理由.
(注:用平行于底的截面截棱錐,該截面與底面之間的部分稱為棱臺,本題中棱臺的體積等于棱錐![]() 的體積減去棱錐
的體積減去棱錐![]() 的體積.)
的體積.)
【答案】(1)證明見解析;(2)![]() ;(3)存在,證明見解析.(注:所構造直平行六面體不唯一,只需題目滿足要求即可)
;(3)存在,證明見解析.(注:所構造直平行六面體不唯一,只需題目滿足要求即可)
【解析】
(1)根據棱長和相等可知![]() ,根據面面平行關系和棱錐為正三棱錐可證得
,根據面面平行關系和棱錐為正三棱錐可證得![]() ,進而證得
,進而證得![]() 各棱長均相等,由此得到結論;(2)取
各棱長均相等,由此得到結論;(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,根據等腰三角形三線合一的性質和線面垂直判定定理可證得
,根據等腰三角形三線合一的性質和線面垂直判定定理可證得![]() 平面
平面![]() ,由線面垂直性質可知
,由線面垂直性質可知![]() ,從而得到
,從而得到![]() 即為所求二面角的平面角;易知
即為所求二面角的平面角;易知![]() ,從而得到
,從而得到![]() ,在
,在![]() 中根據長度關系可求得
中根據長度關系可求得![]() ,從而得到結果;(3)設直平行六面體的棱長均為
,從而得到結果;(3)設直平行六面體的棱長均為![]() ,底面相鄰兩邊夾角為
,底面相鄰兩邊夾角為![]() ,根據正四面體
,根據正四面體![]() 體積為
體積為![]() ,可驗證出
,可驗證出![]() ;又所構造六面體體積為
;又所構造六面體體積為![]() ,知
,知![]() ,只需滿足
,只需滿足![]() 即可滿足要求,從而得到結果.
即可滿足要求,從而得到結果.
(1)![]() 棱臺
棱臺![]() 與棱錐
與棱錐![]() 的棱長和相等
的棱長和相等
![]()
![]() 平面
平面![]() 平面
平面![]() ,三棱錐
,三棱錐![]() 為正三棱錐
為正三棱錐
![]()
![]()
![]()
![]() 為正四面體
為正四面體
(2)取![]() 的中點
的中點![]() ,連接
,連接![]()
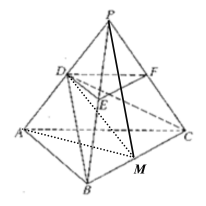
![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 為二面角
為二面角![]() 的平面角
的平面角
由(1)知,![]() 各棱長均為
各棱長均為![]()
![]()
![]() 為
為![]() 中點
中點 ![]()
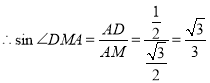
![]()
即二面角![]() 的大小為:
的大小為:![]()
(3)存在滿足題意的直平行六面體,理由如下:
棱臺![]() 的棱長和為定值
的棱長和為定值![]() ,體積為
,體積為![]()
設直平行六面體的棱長均為![]() ,底面相鄰兩邊夾角為
,底面相鄰兩邊夾角為![]()
則該六面體棱長和為![]() ,體積為
,體積為![]()
![]() 正四面體
正四面體![]() 體積為:
體積為:![]()
![]()
![]()
![]() 時,滿足要求
時,滿足要求
故可構造棱長均為![]() ,底面相鄰兩邊夾角為
,底面相鄰兩邊夾角為![]() 的直平行六面體即可滿足要求
的直平行六面體即可滿足要求


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若f (x)在區間(-∞,2)上為單調遞增函數,求實數a的取值范圍;
(2)若a=0,x0<1,設直線y=g(x)為函數f (x)的圖象在x=x0處的切線,求證:f (x)≤g(x).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】未來創造業對零件的精度要求越來越高.![]() 打印通常是采用數字技術材料打印機來實現的,常在模具制造、工業設計等領域被用于制造模型,后逐漸用于一些產品的直接制造,已經有使用這種技術打印而成的零部件.該技術應用十分廣泛,可以預計在未來會有發展空間.某制造企業向
打印通常是采用數字技術材料打印機來實現的,常在模具制造、工業設計等領域被用于制造模型,后逐漸用于一些產品的直接制造,已經有使用這種技術打印而成的零部件.該技術應用十分廣泛,可以預計在未來會有發展空間.某制造企業向![]() 高校
高校![]() 打印實驗團隊租用一臺
打印實驗團隊租用一臺![]() 打印設備,用于打印一批對內徑有較高精度要求的零件.該團隊在實驗室打印出了一批這樣的零件,從中隨機抽取
打印設備,用于打印一批對內徑有較高精度要求的零件.該團隊在實驗室打印出了一批這樣的零件,從中隨機抽取![]() 個零件,度量其內徑的莖葉圖如圖(單位:
個零件,度量其內徑的莖葉圖如圖(單位:![]() ).
).

(1)計算平均值![]() 與標準差
與標準差![]() ;
;
(2)假設這臺![]() 打印設備打印出品的零件內徑
打印設備打印出品的零件內徑![]() 服從正態分布
服從正態分布![]() ,該團隊到工廠安裝調試后,試打了
,該團隊到工廠安裝調試后,試打了![]() 個零件,度量其內徑分別為(單位:
個零件,度量其內徑分別為(單位:![]() ):
):![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,試問此打印設備是否需要進一步調試?為什么?
,試問此打印設備是否需要進一步調試?為什么?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,雙曲線的中心在坐標原點,焦點在![]() 軸上,
軸上,![]() 為雙曲線的頂點,
為雙曲線的頂點,![]() 為雙曲線虛軸的端點,
為雙曲線虛軸的端點,![]() 為右焦點,延長
為右焦點,延長![]() 與
與![]() 交于點
交于點![]() ,若
,若![]() 是銳角,則該雙曲線的離心率的取值范圍是( )
是銳角,則該雙曲線的離心率的取值范圍是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】李明自主創業,在網上經營一家水果店,銷售的水果中有草莓、京白梨、西瓜、桃,價格依次為60元/盒、65元/盒、80元/盒、90元/盒.為增加銷量,李明對這四種水果進行促銷:一次購買水果的總價達到120元,顧客就少付x元.每筆訂單顧客網上支付成功后,李明會得到支付款的80%.
①當x=10時,顧客一次購買草莓和西瓜各1盒,需要支付__________元;
②在促銷活動中,為保證李明每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為 (
(![]() 為參數,
為參數, ![]() ),以
),以![]() 為極點,
為極點, ![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為D的函數![]() ,若同時滿足下列條件:①
,若同時滿足下列條件:①![]() 在D內單調遞增或單調遞減;②存在區間
在D內單調遞增或單調遞減;②存在區間![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() .那么把
.那么把![]() 稱為閉函數.下列結論正確的是( )
稱為閉函數.下列結論正確的是( )
A.函數![]() 是閉函數
是閉函數
B.函數![]() 是閉函數
是閉函數
C.函數![]() 是閉函數
是閉函數
D.![]() 時,函數
時,函數![]() 是閉函數
是閉函數
E.![]() 時,函數
時,函數![]() 是閉函數
是閉函數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com