
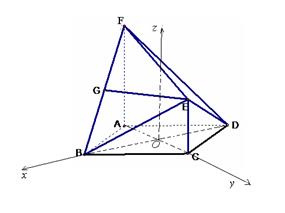
(本小題滿分l2分) 如圖,在多面體ABCDEF中,ABCD為菱形, ABC=60
ABC=60 ,EC
,EC 面ABCD,F(xiàn)A
面ABCD,F(xiàn)A 面ABCD,G為BF的中點,若EG//面ABCD.
面ABCD,G為BF的中點,若EG//面ABCD.
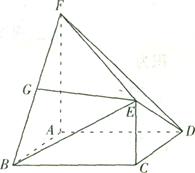
(I)求證:EG 面ABF;
面ABF;
(Ⅱ)若AF=AB,求二面角B—EF—D的余弦值.
(Ⅰ)取AB的中點M,連結(jié)GM,MC,G為BF的中點……;(Ⅱ)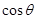 =
=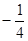 .
.
【解析】
試題分析:(Ⅰ)取AB的中點M,連結(jié)GM,MC,G為BF的中點,
所以GM //FA,又EC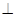 面ABCD, FA
面ABCD, FA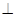 面ABCD,
面ABCD,
∵CE//AF,
∴CE//GM,………………2分
∵面CEGM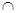 面ABCD=CM,
面ABCD=CM,
EG// 面ABCD,
∴EG//CM,………………4分
∵在正三角形ABC中,CM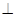 AB,又AF
AB,又AF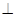 CM
CM
∴EG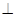 AB, EG
AB, EG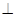 AF,
AF,
∴EG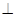 面ABF.…………………6分
面ABF.…………………6分
(Ⅱ)建立如圖所示的坐標系,設(shè)AB=2,
則B(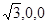 )E(0,1,1) F(0,-1,2)
)E(0,1,1) F(0,-1,2)
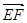 =(0,-2,1) ,
=(0,-2,1) , 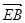 =(
=(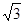 ,-1,-1),
,-1,-1), 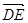 =(
=(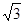 ,1, 1),………………8分
,1, 1),………………8分
設(shè)平面BEF的法向量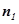 =(
=(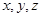 )則
)則
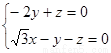 令
令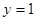 ,則
,則 ,
,
∴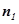 =(
=( )…………………10分
)…………………10分
同理,可求平面DEF的法向量 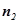 =(-
=(- )
)
設(shè)所求二面角的平面角為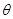 ,則
,則
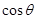 =
=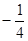 .…………………12分
.…………………12分
考點:本題主要考查立體幾何中線面垂直及角的計算,空間向量的應(yīng)用
點評:典型題,立體幾何中平行、垂直關(guān)系的證明及角的計算問題是高考中的必考題,通過建立適當?shù)淖鴺讼担墒箚栴}簡化。


科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年山東省高三下學(xué)期模擬沖刺考試理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分l2分)已知數(shù)列{an}中,a1=1,a2=3且2an+1=an+2+an(n∈N*).數(shù)列{bn}的前n項和為Sn,其中b1=- ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*).
(1)求數(shù)列{an}和{bn}的通項公式;
(2)若Tn= +
+ +…+
+…+ ,求Tn的表達式
,求Tn的表達式
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年山東省高三下學(xué)期模擬沖刺考試理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分l2分)已知橢圓的的右頂點為A,離心率 ,過左焦點
,過左焦點 作直線
作直線 與橢圓交于點P,Q,直線AP,AQ分別與直線
與橢圓交于點P,Q,直線AP,AQ分別與直線 交于點
交于點 .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)證明以線段 為直徑的圓經(jīng)過焦點
為直徑的圓經(jīng)過焦點 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年貴州省高三年級第五次月考文科數(shù)學(xué) 題型:解答題
(本小題滿分l2分)(注意:在試題卷上作答無效)
求經(jīng)過A(2,-1),和直線x+y=1相切,且圓心在直線y=-2x上的圓的方程
(I)求出圓的標準方程
(II)求出(I)中的圓與直線3x+4y=0相交的弦長AB
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年廣東省高三上學(xué)期10月月考理科數(shù)學(xué)卷 題型:解答題
(本小題滿分l2分)設(shè)命題 :函數(shù)
:函數(shù) (
( )的值域是
)的值域是 ;命題
;命題 :指數(shù)函數(shù)
:指數(shù)函數(shù) 在
在 上是減函數(shù).若命題“
上是減函數(shù).若命題“ 或
或 ”是假命題,求實數(shù)
”是假命題,求實數(shù) 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆山西省高二第二學(xué)期3月月考理科數(shù)學(xué)試卷 題型:解答題
(本小題滿分l2分)求垂直于直線 并且與曲線
并且與曲線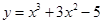 相切的直線方程.
相切的直線方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com