
設(shè)函數(shù)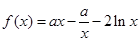 .
.
(1)若 在
在 時(shí)有極值,求實(shí)數(shù)
時(shí)有極值,求實(shí)數(shù) 的值和
的值和 的極大值;
的極大值;
(2)若 在定義域上是增函數(shù),求實(shí)數(shù)
在定義域上是增函數(shù),求實(shí)數(shù) 的取值范圍.
的取值范圍.
(1) 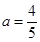 ,
, 的極大值為
的極大值為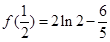 ;(2)
;(2)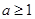 .
.
解析試題分析:(1)由函數(shù)的極值可知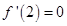 ,對函數(shù)求導(dǎo)
,對函數(shù)求導(dǎo)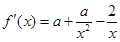 ,將2代入可得
,將2代入可得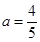 ,則有
,則有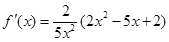 ,令
,令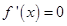 得
得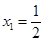 ,
,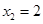 ,
, 在區(qū)間
在區(qū)間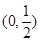 和
和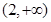 上遞增,在區(qū)間
上遞增,在區(qū)間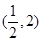 上遞減,所以
上遞減,所以 的極大值為
的極大值為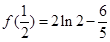 ;(2)
;(2) 在定義域上是增函數(shù),則
在定義域上是增函數(shù),則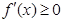 在
在 時(shí)恒成立,又
時(shí)恒成立,又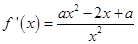 ,則需
,則需 時(shí)
時(shí)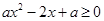 恒成立,即
恒成立,即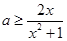 恒成立,
恒成立,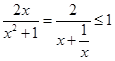 ,可得
,可得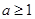 .
.
解:(1)∵ 在
在 時(shí)有極值,∴有
時(shí)有極值,∴有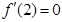
又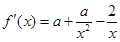 ∴
∴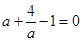 , ∴
, ∴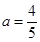 .
.
∴有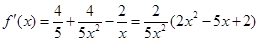
由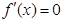 得
得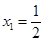 ,
,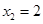
又 ∴由
∴由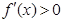 得
得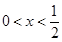 或
或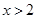
由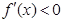 得
得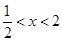
∴ 在區(qū)間
在區(qū)間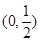 和
和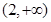 上遞增,在區(qū)間
上遞增,在區(qū)間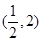 上遞減
上遞減
∴ 的極大值為
的極大值為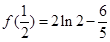
(2)若 在定義域上是增函數(shù),則
在定義域上是增函數(shù),則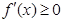 在
在 時(shí)恒成立
時(shí)恒成立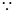
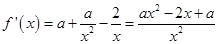 ,
,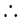 需
需 時(shí)
時(shí)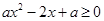 恒成立,
恒成立,
化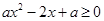 為
為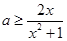 恒成立,
恒成立,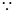
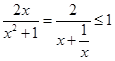 ,
, 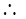
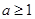 為所求.
為所求.
考點(diǎn):函數(shù)的極值.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)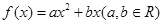 ,函數(shù)
,函數(shù)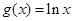 .
.
⑴當(dāng)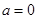 時(shí),函數(shù)
時(shí),函數(shù) 的圖象與函數(shù)
的圖象與函數(shù)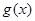 的圖象有公共點(diǎn),求實(shí)數(shù)
的圖象有公共點(diǎn),求實(shí)數(shù)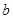 的最大值;
的最大值;
⑵當(dāng)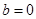 時(shí),試判斷函數(shù)
時(shí),試判斷函數(shù) 的圖象與函數(shù)
的圖象與函數(shù)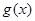 的圖象的公共點(diǎn)的個(gè)數(shù);
的圖象的公共點(diǎn)的個(gè)數(shù);
⑶函數(shù) 的圖象能否恒在函數(shù)
的圖象能否恒在函數(shù)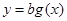 的上方?若能,求出
的上方?若能,求出 的取值范圍;若不能,請說明理由.
的取值范圍;若不能,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)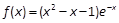 .
.
(1)求f(x)的單調(diào)區(qū)間和極值;
(2)關(guān)于 的方程f(x)=a在區(qū)間
的方程f(x)=a在區(qū)間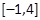 上有兩個(gè)根,求a的取值范圍.
上有兩個(gè)根,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù)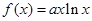
 ,已知曲線
,已知曲線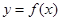 在點(diǎn)
在點(diǎn)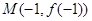 處的切線方程是
處的切線方程是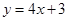 .
.
(1)求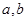 的值;并求出函數(shù)的單調(diào)區(qū)間;
的值;并求出函數(shù)的單調(diào)區(qū)間;
(2)求函數(shù) 在區(qū)間
在區(qū)間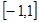 上的最值.
上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)函數(shù) ,其導(dǎo)函數(shù)為
,其導(dǎo)函數(shù)為 .
.
(1)若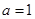 ,求函數(shù)
,求函數(shù) 在點(diǎn)
在點(diǎn) 處的切線方程;
處的切線方程;
(2)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若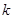 為整數(shù),若
為整數(shù),若 時(shí),
時(shí), 恒成立,試求
恒成立,試求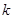 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)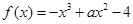 (
(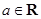 ).
).
⑴ 若函數(shù)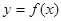 的圖象在點(diǎn)
的圖象在點(diǎn)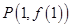 處的切線的傾斜角為
處的切線的傾斜角為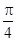 ,求
,求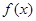 在
在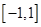 上的最小值;
上的最小值;
⑵ 若存在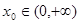 ,使
,使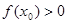 ,求
,求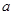 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,曲線
,曲線 在點(diǎn)
在點(diǎn)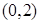 處的切線與
處的切線與 軸交點(diǎn)的橫坐標(biāo)為
軸交點(diǎn)的橫坐標(biāo)為 .
.
(1)求 ;
;
(2)證明:當(dāng) 時(shí),曲線
時(shí),曲線 與直線
與直線 只有一個(gè)交點(diǎn).
只有一個(gè)交點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)f(x)是定義在區(qū)間(1,+∞)上的函數(shù),其導(dǎo)函數(shù)為f′(x).如果存在實(shí)數(shù)a和函數(shù)h(x),其中h(x)對任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),則稱函數(shù)f(x)具有性質(zhì)P(a).
(1)設(shè)函數(shù)f(x)=ln x+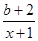 (x>1),其中b為實(shí)數(shù).
(x>1),其中b為實(shí)數(shù).
①求證:函數(shù)f(x)具有性質(zhì)P(b);
②求函數(shù)f(x)的單調(diào)區(qū)間;
(2)已知函數(shù)g(x)具有性質(zhì)P(2).給定x1,x2∈(1,+∞),x1<x2,設(shè)m為實(shí)數(shù),α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α)-g(β)|<|g(x1)-g(x2)|,求m的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com