
【題目】已知函數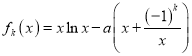 .
.
(1)當![]() 時,求
時,求![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)對于任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)試討論函數![]() 的極值點的個數.
的極值點的個數.
【答案】(1)![]() (2)
(2)![]() (3)解答見解析
(3)解答見解析
【解析】
(1)由題意,當![]() 時,可得
時,可得![]() ,求得
,求得![]() ,且
,且![]() ,利用點斜式方程,即可求解;
,利用點斜式方程,即可求解;
(2)由![]() ,
,![]() 恒成立,轉化為即
恒成立,轉化為即![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,利用導數求得函數
,利用導數求得函數![]() 的單調性與最值,即可求解;
的單調性與最值,即可求解;
(3)由![]()
![]() ,得到則
,得到則![]() ,令
,令![]() ,得到
,得到![]() ,對
,對![]() 分類討論,即可求解.
分類討論,即可求解.
(1)由題意,當![]() 時,函數
時,函數![]() ,
,
則![]() ,可得
,可得![]() ,且
,且![]() ,
,
所以![]() 在
在![]() 處的切線方程
處的切線方程![]() .
.
(2)由![]() ,
,![]() 恒成立,
恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,則
,則![]() ,
,
當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,
當![]() ,即
,即![]() 時,令
時,令![]() ,得
,得![]() (
(![]() 舍去).
舍去).
|
|
|
|
| - | 0 | + |
|
|
|
所以當![]() 時,
時,![]() ,不符合題意.
,不符合題意.
綜上可得,![]() ,即
,即![]() 的取值范圍
的取值范圍![]() .
.
(3)由![]()
![]() ,
,
則![]() ,
,
令![]() ,則
,則![]() ,
,
①當![]() ,即
,即![]() 時,
時,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
且![]() ,
,![]() .
.
由零點存在性定理可知![]() 在
在![]() 上存在唯一的零點,不妨設為
上存在唯一的零點,不妨設為![]() .
.
|
|
|
|
| - | 0 | + |
|
| 極小值 |
|
所以函數![]() 有一個極值點;
有一個極值點;
②當![]() ,即
,即![]() 時,令
時,令![]() ,則
,則![]() .
.
|
|
|
|
| - | 0 | + |
|
| 極小值 |
|
所以函數![]() 的最小值為
的最小值為![]() .
.
1*)當![]() ,即
,即![]() 時,
時,![]() 恒成立,
恒成立,
令![]() ,
,
由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,得
上單調遞減,得![]() ,
,
∴![]() ,
,
∴![]() 單調遞增,無極值點,即
單調遞增,無極值點,即![]() 時,
時,![]() 無極值點.
無極值點.
2*)當![]() ,即
,即![]() 時,且
時,且![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上有唯一的零點
上有唯一的零點![]() .
.
下面先證:![]() .
.
設![]() ,∴
,∴![]() ,
,
當![]() 時,
時,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() 單調遞增,
單調遞增,
所以![]() ,即
,即![]() 得證,
得證,
所以
![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
由零點存在性定理可知![]() 在
在![]() 上存在唯一零點,不妨設
上存在唯一零點,不妨設![]() ,
,
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
|
|
|
|
所以函數![]() 有兩個極值點;
有兩個極值點;
3*)當![]() 時,
時,![]() 且
且![]() ,
,![]() ,
,![]() ,
,
又由![]() ,
,
∴由零點存在性定理可知![]() 在
在![]() 與
與![]() 上各存在唯一零點,
上各存在唯一零點,
同上2*)可知![]() 有兩個極值點.
有兩個極值點.
綜上所述,當![]() 時,
時,![]() 有一個極值點;當
有一個極值點;當![]() 且
且![]() 時,
時,![]() 有兩個極值點;當
有兩個極值點;當![]() 時,
時,![]() 無極值點.
無極值點.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知拋物線y2=2px(p>0)上一點P![]() 到準線的距離與到原點O的距離相等,拋物線的焦點為F.
到準線的距離與到原點O的距離相等,拋物線的焦點為F.
(1)求拋物線的方程;
(2)若A為拋物線上一點(異于原點O),點A處的切線交x軸于點B,過A作準線的垂線,垂足為點E,試判斷四邊形AEBF的形狀,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,已知曲線![]() ,將曲線
,將曲線![]() 上的點向左平移一個單位,然后縱坐標不變,橫坐標軸伸長到原來的2倍,得到曲線
上的點向左平移一個單位,然后縱坐標不變,橫坐標軸伸長到原來的2倍,得到曲線![]() ,又已知直線
,又已知直線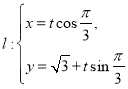 (
(![]() 是參數),且直線
是參數),且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(I)求曲線![]() 的直角坐標方程,并說明它是什么曲線;
的直角坐標方程,并說明它是什么曲線;
(II)設定點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題,其中正確的是( )
A.對分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 的觀測值
的觀測值![]() 來說,
來說,![]() 越小,“
越小,“![]() 與
與![]() 有關系”可信程度越大
有關系”可信程度越大
B.殘差點比較均勻地落在水平帶狀區域內,帶狀區域越窄,則模型擬合精度越高
C.相關指數![]() 越小,則殘差平方和越大,模型的擬合效果越好
越小,則殘差平方和越大,模型的擬合效果越好
D.兩個隨機變量相關性越強,則相關系數的絕對值越接近![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究性學習小組對無現金支付(支付寶、微信、銀行卡)的用戶進行問卷調查,隨機選取了![]() 人(圖1),按年齡分為青年組與中老年組,如圖2.
人(圖1),按年齡分為青年組與中老年組,如圖2.
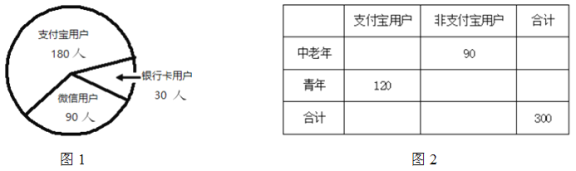
(1)完成圖2的列聯表,并判斷是否有![]() 的把握認為使用支付寶用戶與年齡有關系?
的把握認為使用支付寶用戶與年齡有關系?
(2)現從調查的中老年組中按分層抽樣的方法選出![]() 人,再隨機抽取
人,再隨機抽取![]() 人贈送禮品,試求抽取的
人贈送禮品,試求抽取的![]() 人中恰有
人中恰有![]() 人為“非支付寶用戶”的概率.
人為“非支付寶用戶”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各進行3次射擊,甲每次擊中目標的概率為![]() ,乙每次擊中目標的概率為
,乙每次擊中目標的概率為![]() 。
。
(1)記甲擊中目標的次數為![]() ,求
,求![]() 的概率分布及數學期望;
的概率分布及數學期望;
(2)求乙至多擊目標2次的概率;
(3)求甲恰好比乙多擊中目標2次的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年10月中上旬是小麥的最佳種植時間,但小麥的發芽會受到土壤、氣候等多方面因素的影響.某科技小組為了解晝夜溫差的大小與小麥發芽的多少之間的關系,在不同的溫差下統計了100顆小麥種子的發芽數,得到了如下數據:
溫差 | 8 | 10 | 11 | 12 | 13 |
發芽數 | 79 | 81 | 85 | 86 | 90 |
(1)請根據統計的最后三組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由(1)中的線性回歸方程得到的估計值與前兩組數據的實際值誤差均不超過兩顆,則認為線性回歸方程是可靠的,試判斷(1)中得到的線性回歸方程是否可靠;
(3)若100顆小麥種子的發芽率為![]() 顆,則記為
顆,則記為![]() 的發芽率,當發芽率為
的發芽率,當發芽率為![]() 時,平均每畝地的收益為
時,平均每畝地的收益為![]() 元,某農場有土地10萬畝,小麥種植期間晝夜溫差大約為
元,某農場有土地10萬畝,小麥種植期間晝夜溫差大約為![]() ,根據(1)中得到的線性回歸方程估計該農場種植小麥所獲得的收益.
,根據(1)中得到的線性回歸方程估計該農場種植小麥所獲得的收益.
附:在線性回歸方程![]() 中,
中,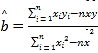 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com