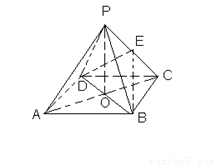
（本題8分）如圖，ABCD是正方形，O是正方形的中心， PO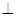
底面ABCD，E是PC的中點。
求證：（1）PA∥平面BDE （2）平面PAC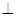平面BDE
見解析。
【解析】本題主要考查中位線定理、線面平行的判定定理和面面垂直的判定定理．考查立體幾何的基本定理和空間想象能力
（1）先根據中位線定理得到OE∥AP，進而再由線面平行的判定定理可得到PA∥平面BDE．
（2）先根據線面垂直的性質定理得到PO⊥BD，結合AC⊥BD根據線面垂直的判定定理得到BD⊥平面PAC，從而根據面面垂直的判定定理得到平面PAC⊥平面BDE，得證．
證明：（1）連結E0
四邊形ABCD為正方形
O為AC的中點 又E是PC的中點
EO//PA
PA//平面BDE
4分
（2）
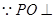平面ABCD，
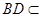平面ABCD
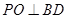
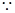四邊形ABCD是正方形
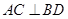
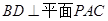，又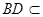
平面BDE
平面PAC
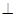平面BDE
4分
黃岡小狀元解決問題天天練系列答案
三點一測快樂周計劃系列答案科目：高中數學 來源：2011年安徽省師大附中高一第一學期期中考試數學 題型：解答題
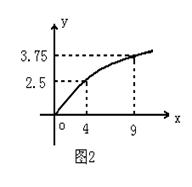
(本題8分)某民營企業生產A，B兩種產品，根據市場調查和預測，A產品的利潤與投資成正比，其關系如圖1，B產品的利潤與投資的算術平方根成正比，其關系如圖2（注：利潤與投資單位是萬元）
（1）分別將A，B兩種產品的利潤表
示為投資的函數，并寫出它們的函數關系式
（2）該企業已籌集到10萬元資金，并全部投入A，B兩種產品的生產，問：怎樣分配這10萬元投資，才能是企業獲得最大利潤，其最大利潤約為多少萬元（精確到1萬元）.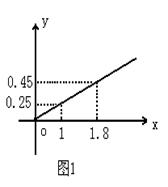
查看答案和解析>>
科目：高中數學 來源：2013屆浙江省嘉興市八校高二上期中聯考理科數學試卷（解析版） 題型：解答題
（本題8分）如圖，已知點A(2,3), B(4,1)，△ABC是以AB為底邊的等腰三角形，點C在直線l：x－2y＋2＝0上．
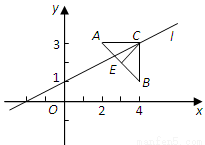
（Ⅰ）求AB邊上的高CE所在直線的方程；
（Ⅱ）求△ABC的面積．
查看答案和解析>>
科目：高中數學 來源：2011年安徽省高一第一學期期中考試數學 題型：解答題
(本題8分)某民營企業生產A，B兩種產品，根據市場調查和預測，A產品的利潤與投資成正比，其關系如圖1，B產品的利潤與投資的算術平方根成正比，其關系如圖2（注：利潤與投資單位是萬元）
（1）分別將A，B兩種產品的利潤表示為投資的函數，并寫出它們的函數關系式
（2）該企業已籌集到10萬元資金，并全部投入A，B兩種產品的生產，問：怎樣分配這10萬元投資，才能是企業獲得最大利潤，其最大利潤約為多少萬元（精確到1萬元）.
查看答案和解析>>
科目：高中數學 來源：2010年海南省高一期中考試數學試卷 題型：解答題
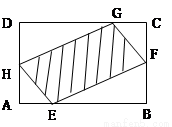
（本題滿分8分）如圖，有一塊矩形空地，要在這塊空地上辟一個內接四邊形為綠地，使其四個頂點分別落在矩形的四條邊上，已知AB＝a（a>2），BC＝2，且AE＝AH＝CF＝CG，設AE＝x，綠地面積為y．
(Ⅰ)寫出y關于x的函數關系式，并指出這個函數的定義域；
(Ⅱ)當AE為何值時，綠地面積最大？
查看答案和解析>>
科目：高中數學 來源：2010年山東省北校區高二上學期第一次月考數學卷 題型：解答題
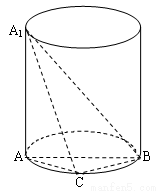
（本題滿分8分）如圖，A1A是圓柱的母線，AB是圓柱底面圓的直徑， C是底面圓周上異于A，B的任意一點，A1A= AB=2.
（Ⅰ）求證: BC⊥平面A1AC；
（Ⅱ）求三棱錐A1-ABC的體積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com