【題目】已知函數(shù)
.
（1）若
， 
都是從0，1，2，3，4五個數(shù)中任取的一個數(shù)，求上述函數(shù)有零點的概率；
（2）若
， 
都是從區(qū)間
上任取的一個數(shù)，求
成立的概率.
【答案】（1）
（2）
【解析】試題分析：
(1)基本事件總數(shù)為
個.函數(shù)有零點的條件為
.
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，則函數(shù)
有零點的概率為
.
(2)由幾何概型的計算公式可得事件“
”的概率為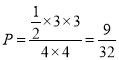
.
試題解析：
解：（1）
， 
都是從0，1，2，3，4五個數(shù)中任取的一個數(shù)，則基本事件總數(shù)為
個.
函數(shù)有零點的條件為
，即
.因為事件“
”包含
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，
所以事件“
”的概率為
，即函數(shù)
有零點的概率為
.
（2）
， 
都是從區(qū)間
上任取的一個數(shù)， 
，即
，此為幾何模型，如圖可知，事件“
”的概率為
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
．
（1）求證：不論
為何實數(shù)
總為增函數(shù)；
（2）確定的值，使為奇函數(shù)；
（3）在（2）的條件下求的值域．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，
是平行四邊形，
，
為
的中點，且有
，現(xiàn)以
為折痕，將
折起，使得點
到達點
的位置，且
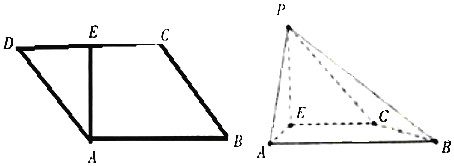
（1）證明：
平面
；
（2）若四棱錐
的體積為
，求四棱錐的側(cè)面積．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】從某企業(yè)生產(chǎn)的某種產(chǎn)品中抽取500件，測量這些產(chǎn)品的一項質(zhì)量指標值，由測量結(jié)果得如下頻率分布直方圖：
（1）求這500件產(chǎn)品質(zhì)量指標值的樣本平均數(shù) 
和樣本方差s2（同一組中數(shù)據(jù)用該組區(qū)間的中點值作代表）；
（2）由直方圖可以認為，這種產(chǎn)品的質(zhì)量指標值Z服從正態(tài)分布N（μ，σ2），其中μ近似為樣本平均數(shù) ，σ2近似為樣本方差s2 ．
（i）利用該正態(tài)分布，求P（187.8＜Z＜212.2）；
（ii）某用戶從該企業(yè)購買了100件這種產(chǎn)品，記X表示這100件產(chǎn)品中質(zhì)量指標值位于區(qū)間（187.8，212.2）的產(chǎn)品件數(shù)，利用（i）的結(jié)果，求EX．
附： 
≈12.2．
若Z～N（μ，σ2）則P（μ﹣σ＜Z＜μ+σ）=0.6826，P（μ﹣2σ＜Z＜μ+2σ）=0.9544．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
的前n項和
．
若三角形的三邊長分別為
，
，
，求此三角形的面積；
探究數(shù)列中是否存在相鄰的三項，同時滿足以下兩個條件：
此三項可作為三角形三邊的長；
此三項構(gòu)成的三角形最大角是最小角的2倍
若存在，找出這樣的三項，若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列三個命題中
①“k=1”是“函數(shù)y=cos2kx-sin2kx的最小正周期為π”的充要條件;
②“a=3”是“直線ax+2y+3a=0與直線3x+(a-1)y=a-7相互垂直”的充要條件;
③“雙曲線
上任意點M到兩條漸近線距離的積為定值”的逆否命題
其中是真命題的為________
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】一中最強大腦社對高中學(xué)生的記憶力
和判斷力
進行統(tǒng)計分析，得下表數(shù)據(jù)
參考公式：
，
.
（1）請根據(jù)上表提供的數(shù)據(jù)，用最小二乘法求出關(guān)于的線性回歸方程
，預(yù)測記憶力為
的同學(xué)的判斷力．
（2）若記憶力增加
個單位，預(yù)測判斷力增加多少個單位？
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
