【答案】
分析:(I)由題意,
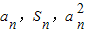
成等差數列,可得
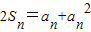
(n∈N
*),再寫一式,兩式相減,整理可得a
n+1-a
n=1,即{a
n}為公差為1的等差數列,再確定數列的首項.即可求得數列{a
n}的通項a
n;
(II)
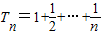
,當n≥2時,R
n-1=1+(1+

)+…+(
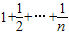
)=n-1+
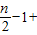

+
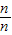
-1=n(
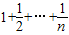
)-n,即可證得結論;
(III)先證明
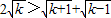
,再證明當k≥2時,
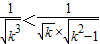
<
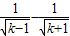
,利用疊加法,即可求得結論.
解答:(I)解:由題意,
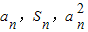
成等差數列,∴
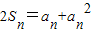
(n∈N
*).
于是
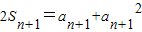
,
兩式相減,得
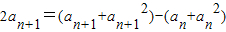
,
即a
n+1+a
n=(a
n+1+a
n)(a
n+1-a
n),
由題,a
n>0,a
n+1+a
n≠0,
得a
n+1-a
n=1,即{a
n}為公差為1的等差數列.
又由
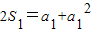
,得a
1=1或a
1=0(舍去).
∴a
n=1+(n-1)•1=n (n∈N
*).…(5分)
(II)證明:由(I)知
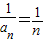
,于是
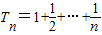
,
于是當n≥2時,R
n-1=1+(1+

)+…+(
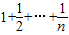
)=n-1+
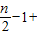
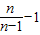
+
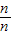
-1
=n(
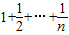
)-n=n(T
n-1).…(10分)
(III)解:由(I)知,
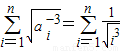
.
∵
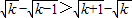
,∴
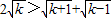
,
當k≥2時,
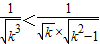
<
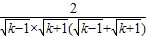
=
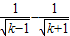
,
∴
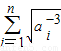
<1+(1-
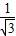
)+(
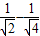
)+…+(
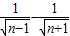
)=2+
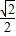
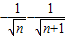
.
即較
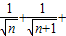
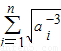
<2+
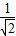
. …(14分)
點評:本題考查數列遞推式,考查數列的通項,考查不等式的證明,考查放縮法的運用,解題的關鍵是正確放縮,屬于中檔題.

 成等差數列.
成等差數列. }的前n項和為Tn,數列{Tn}的前n項和為Rn,求證:當n≥2,n∈N*時,Rn-1=n(Tn-1);
}的前n項和為Tn,數列{Tn}的前n項和為Rn,求證:當n≥2,n∈N*時,Rn-1=n(Tn-1);
 與2+
與2+ 的大小.
的大小.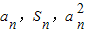 成等差數列,可得
成等差數列,可得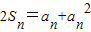 (n∈N*),再寫一式,兩式相減,整理可得an+1-an=1,即{an}為公差為1的等差數列,再確定數列的首項.即可求得數列{an}的通項an;
(n∈N*),再寫一式,兩式相減,整理可得an+1-an=1,即{an}為公差為1的等差數列,再確定數列的首項.即可求得數列{an}的通項an;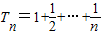 ,當n≥2時,Rn-1=1+(1+
,當n≥2時,Rn-1=1+(1+ )+…+(
)+…+(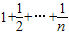 )=n-1+
)=n-1+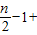
 +
+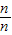 -1=n(
-1=n(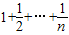 )-n,即可證得結論;
)-n,即可證得結論;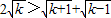 ,再證明當k≥2時,
,再證明當k≥2時,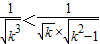 <
<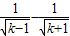 ,利用疊加法,即可求得結論.
,利用疊加法,即可求得結論.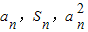 成等差數列,∴
成等差數列,∴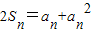 (n∈N*).
(n∈N*).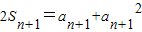 ,
,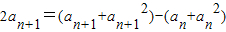 ,
,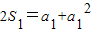 ,得a1=1或a1=0(舍去).
,得a1=1或a1=0(舍去).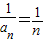 ,于是
,于是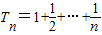 ,
, )+…+(
)+…+(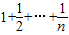 )=n-1+
)=n-1+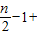
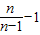 +
+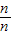 -1
-1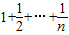 )-n=n(Tn-1).…(10分)
)-n=n(Tn-1).…(10分)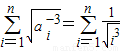 .
.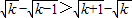 ,∴
,∴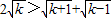 ,
,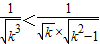 <
<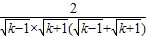 =
=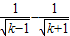 ,
,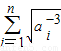 <1+(1-
<1+(1-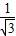 )+(
)+(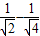 )+…+(
)+…+(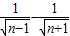 )=2+
)=2+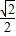
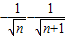 .
.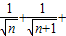
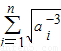 <2+
<2+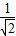 . …(14分)
. …(14分)

 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案