【題目】若函數f（x）＝x2+x﹣lnx+1在其定義域的一個子區間（2k﹣1，k+2）內不是單調函數，則實數k的取值范圍是___．
【答案】
.
【解析】
根據題意，求出函數
的定義域，由區間（2k﹣1，k+2）為其定義域的一個子區間得到關于
的不等式，對函數進行求導，利用導數判斷函數的單調區間，結合函數在區間（2k﹣1，k+2）上不單調得到關于的不等式，然后取交集即可.
由題意知，函數f（x）＝x2+x﹣lnx+1的定義域為（0，+∞），
由區間（2k﹣1，k+2）為其定義域的一個子區間，可得：0≤2k﹣1＜k+2，解得
≤k＜3，
f′（x）＝2x+1﹣
，令f′（x）＝0，解得x＝，
所以當
時，
，函數在
上單調遞減；
當
時，
，函數在
上單調遞增，
∵函數f（x）＝x2+x﹣lnx+1在其定義域的一個子區間（2k﹣1，k+2）內不是單調函數，
∴2k﹣1＜＜k+2，解得：﹣
＜k＜
，與≤k＜3聯立解得：≤k＜．
故答案為：.
科目：高中數學 來源： 題型：
【題目】我國古代數學名著《孫子算經》中有如下問題：“今有三女，長女五日一歸，中女四日一歸，少女三日一歸．問：三女何日相會？”意思是：“一家出嫁的三個女兒中，大女兒每五天回一次娘家，二女兒每四天回一次娘家，小女兒每三天回一次娘家．三個女兒從娘家同一天走后，至少再隔多少天三人再次相會？”假如回娘家當天均回夫家，若當地風俗正月初二都要回娘家，則從正月初三算起的一百天內，有女兒回娘家的天數有（ ）
A.58B.59C.60D.61
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數學名著《算學啟蒙》中有關于“松竹并生”的問題：松長四尺，竹長兩尺，松日自半，竹日自倍，松竹何日而長等.如圖，是源于其思想的一個程序框圖.若輸入的
分別為8、2，則輸出的
（ ）
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖給出的是2000年至2016年我國實際利用外資情況，以下結論正確的是（ ）
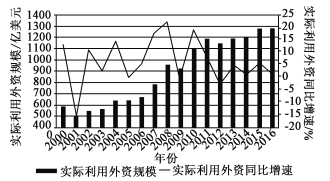
A. 2000年以來我國實際利用外資規模與年份呈負相關
B. 2010年以來我國實際利用外資規模逐年增大
C. 2008年以來我國實際利用外資同比增速最大
D. 2010年以來我國實際利用外資同比增速最大
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將函數
圖象上所有點的橫坐標縮短為原來的
，縱坐標不變，再向右平移
個單位長度，得到函數
的圖象，則下列說法正確的是（ ）
A. 函數
的一條對稱軸是
B. 函數的一個對稱中心是
C. 函數的一條對稱軸是
D. 函數的一個對稱中心是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線的頂點在原點,過點A(-4,4)且焦點在x軸.
（1）求拋物線方程;
（2）直線l過定點B(-1,0)與該拋物線相交所得弦長為8,求直線l的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖是我國2010年至2016年生活垃圾無害化處理量（單位：億噸）的折線圖
注：年份代碼1~7分別對應年份2010~2016
（1）由折線圖看出，可用線性回歸模型擬合y與t的關系，請求出相關系數r，并用相關系數的大小說明y與t相關性的強弱；
（2）建立y關于t的回歸方程（系數精確到0.01），預測2018年我國生活垃圾無害化處理量.
附注：
參考數據：
，
，
， 
.
參考公式：
相關系數
回歸方程
中斜率和截距的最小二乘估計公式分別為：
查看答案和解析>>
科目：高中數學 來源： 題型：
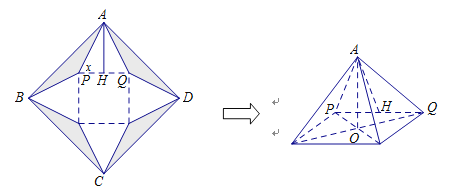
【題目】如圖：設一正方形紙片ABCD邊長為2分米，切去陰影部分所示的四個全等的等腰三角形，剩余為一個正方形和四個全等的等腰三角形，沿虛線折起，恰好能做成一個正四棱錐（粘接損耗不計），圖中
，O為正四棱錐底面中心．
（Ⅰ）若正四棱錐的棱長都相等，求這個正四棱錐的體積Ｖ；
（Ⅱ）設等腰三角形APQ的底角為x，試把正四棱錐的側面積S表示為x的函數，并求S的范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
