等差數(shù)列{
an}共有2n+1項,其中奇數(shù)項之和為4,偶數(shù)項之和為3,則n的值是
試題分析:利用等差數(shù)列的求和公式和性質(zhì)得出

,來解得。解:設數(shù)列公差為d,首項為a
1,奇數(shù)項共n+1項,其和為S
奇=(n+1)a
n+1=4,偶數(shù)項共n項,其和為S
偶=na
n+1=3,由

,可知n的值為3,選A.
點評:本題考查等差數(shù)列的求和公式和性質(zhì),熟練記憶并靈活運用求和公式是解題的關鍵,屬基礎題
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
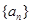
是一個等差數(shù)列,
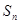
是其前
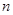
項和,且
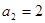
,
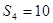
.
(1)求
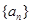
的通項
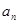
;
(2)求數(shù)列
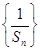
的前10項的和
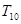
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
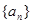
的前
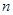
項和
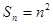
,數(shù)列
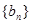
滿足
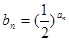
(1)求數(shù)列
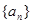
的通項公式
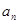
;(2)求數(shù)列
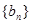
的前
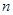
項和
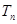
;
(3)求證:不論
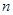
取何正整數(shù),不等式
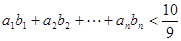
恒成立
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
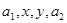
成等差數(shù)列,
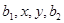
成等比數(shù)列.則
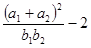
的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設Sn是等差數(shù)列{
an}的前n項和,已知
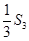
與
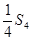
的等比中項為
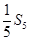
,
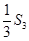
與
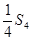
的等差中項為1,求等差數(shù)列{
an}的通項。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若兩個等差數(shù)列
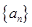
、
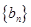
的前
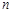
項和分別為
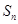
、
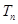
,對任意的
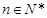
都
有
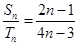
,則
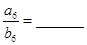
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
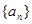
的首項為
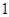
,對任意的
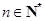
,定義
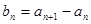
.
(Ⅰ) 若
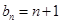
,
(i)求
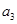
的值和數(shù)列
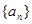
的通項公式;
(ii)求數(shù)列
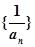
的前
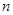
項和
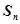
;
(Ⅱ)若
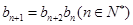
,且
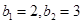
,求數(shù)列
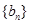
的前
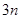
項的和.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設等差數(shù)列

的前n項和為

,若

,則當

取最小值時,n等于________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知方程tan
2x一
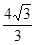
tan x+1=0在x
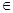
[0,n
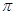
)( n
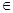
N*)內(nèi)所有根的和記為a
n(1)寫出a
n的表達式;(不要求嚴格的證明)
(2)記S
n = a
1 + a
2 +…+ a
n求S
n;
(3)設b
n =(kn一5)
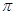
,若對任何n
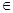
N* 都有a
n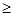
b
n,求實數(shù)k的取值范圍.
查看答案和解析>>

 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案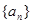 的前
的前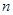 項和
項和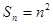 ,數(shù)列
,數(shù)列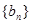 滿足
滿足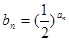
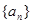 的通項公式
的通項公式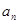 ;(2)求數(shù)列
;(2)求數(shù)列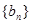 的前
的前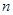 項和
項和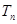 ;
;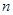 取何正整數(shù),不等式
取何正整數(shù),不等式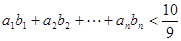 恒成立
恒成立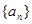 的首項為
的首項為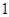 ,對任意的
,對任意的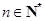 ,定義
,定義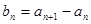 .
.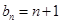 ,
,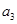 的值和數(shù)列
的值和數(shù)列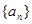 的通項公式;
的通項公式;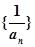 的前
的前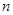 項和
項和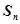 ;
;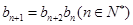 ,且
,且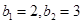 ,求數(shù)列
,求數(shù)列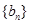 的前
的前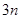 項的和.
項的和.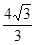 tan x+1=0在x
tan x+1=0在x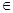 [0,n
[0,n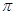 )( n
)( n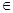 N*)內(nèi)所有根的和記為an
N*)內(nèi)所有根的和記為an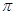 ,若對任何n
,若對任何n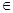 N* 都有an
N* 都有an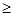 bn,求實數(shù)k的取值范圍.
bn,求實數(shù)k的取值范圍.