Question

有四條線段，長度分別是2cm，3cm，4cm，5cm，從中任取三條，能構成三角形的概率是    ．

Answer 1

【答案】分析：由四條線段中任意取3條，是一個無放回列舉法求概率問題，列出構成三角形種數，因而就可求出概率．
解答：解：由四條線段中任意取3條，是一個列舉法求概率問題，是無放回的問題，共有4×3×2=24種可能結果，每種結果出現的機會相同，其中不滿足兩邊之和大于第三邊的有：2cm，3cm，5cm；
2cm，5cm，3cm；
3cm，2cm，5cm；
3cm，5cm，2cm；
5cm，2cm，3cm；
5cm，3cm，2cm  共6種，則滿足的有24-6=18種，
∴P（任取三條，能構成三角形）=．
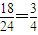
故填：．
點評：本題是一個列舉法求概率與三角形的三邊關系相結合的題目；情況較少可用列舉法求概率，采用列舉法解題的關鍵是找到所有存在的情況．用到的知識點為：概率=所求情況數與總情況數之比．組成三角形的兩小邊之和大于最大的邊長．
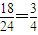