
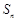 是等比數(shù)列
是等比數(shù)列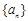 的前
的前 項(xiàng)和,
項(xiàng)和,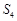 、
、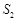 、
、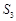 成等差數(shù)列,且
成等差數(shù)列,且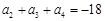 .
.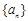 的通項(xiàng)公式;
的通項(xiàng)公式; ,使得
,使得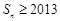 ?若存在,求出符合條件的所有
?若存在,求出符合條件的所有 的集合;若不存在,說(shuō)明理由.
的集合;若不存在,說(shuō)明理由.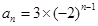 ;(2)存在符合條件的正整數(shù)
;(2)存在符合條件的正整數(shù) 的集合為
的集合為 .
. 的公比為
的公比為 ,依題意,列出關(guān)于首項(xiàng)
,依題意,列出關(guān)于首項(xiàng) 與公比
與公比 的方程組,解之即可求得數(shù)列
的方程組,解之即可求得數(shù)列 的通項(xiàng)公式;(2)依題意,可得
的通項(xiàng)公式;(2)依題意,可得 ,對(duì)
,對(duì) 的奇偶性進(jìn)行分類討論,即可求得答案.
的奇偶性進(jìn)行分類討論,即可求得答案.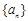 的公比為
的公比為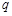 ,則
,則 ,
,
 即
即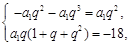 解得
解得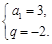
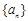 的通項(xiàng)公式為
的通項(xiàng)公式為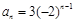 6分
6分 7分
7分 ,使得
,使得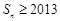 ,則
,則 ,即
,即 8分
8分 為偶數(shù)時(shí),
為偶數(shù)時(shí),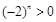 ,上式不成立 9分
,上式不成立 9分 為奇數(shù)時(shí),
為奇數(shù)時(shí), ,即
,即 ,則
,則 11分
11分 的集合為
的集合為 12分.
12分.


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
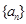 的公比為q,且
的公比為q,且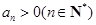 ,
,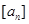 表示不超過(guò)實(shí)數(shù)
表示不超過(guò)實(shí)數(shù)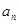 的最大整數(shù)(如
的最大整數(shù)(如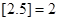 ),記
),記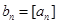 ,數(shù)列
,數(shù)列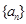 的前
的前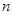 項(xiàng)和為
項(xiàng)和為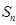 ,數(shù)列
,數(shù)列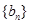 的前
的前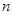 項(xiàng)和為
項(xiàng)和為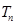 .
.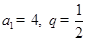 ,求
,求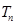 ;
;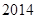 的正整數(shù)n,都有
的正整數(shù)n,都有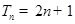 ,證明:
,證明: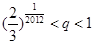 .
.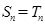 (
(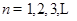 )的充分必要條件為
)的充分必要條件為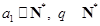 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:解答題
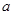 為實(shí)數(shù),數(shù)列
為實(shí)數(shù),數(shù)列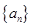 滿足
滿足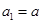 ,當(dāng)
,當(dāng)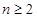 時(shí),
時(shí),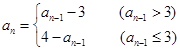 ,
, 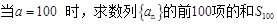 ;(5分)
;(5分)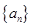 ,一定存在
,一定存在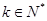 ,使
,使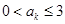 ;(5分)
;(5分)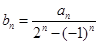 ,當(dāng)
,當(dāng)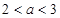 時(shí),求證:
時(shí),求證: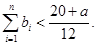 (6分)
(6分)查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
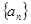 的各項(xiàng)都是正數(shù),且
的各項(xiàng)都是正數(shù),且 =16,則
=16,則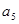 =( ).
=( ).| A.1 | B.2 | C.4 | D.8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:單選題
| A.4 | B.5 | C.6 | D.7 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:不詳 題型:填空題
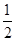 ,a4=-4,則|a1|+|a2|+…+|an|=________.
,a4=-4,則|a1|+|a2|+…+|an|=________.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com