Question

已知A（1，2），B（3，4），直線l₁：x=0，l₂：y=0和l₃：x+3y-1=0、設P_i是l_i（i=1，2，3）上與A、B兩點距離平方和最小的點，則△P₁P₂P₃的面積是    ．

Answer 1

【答案】分析：設出P₁，P₂，P₃，求出P₁到A，B兩點的距離和最小時，P₁坐標，求出P₂，P₃的坐標，然后再解三角形的面積即可．
解答：解：設P₁（0，b），P₂（a，0），P₃（x，y）
由題設點P₁到A，B兩點的距離和為
d=3²+（4-b）²+1²+（2-b）²=2（b-3）²+12
顯然當b=3即P₁（0，3）時，點P₁到A，B兩點的距離和最小
同理P₂（2，0），P₃（1，0），所以
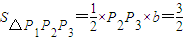
故答案為：
點評：本題考查得到直線的距離公式，函數的最值，考查函數與方程的思想，是中檔題．