
【題目】從某小區抽取50戶居民進行月用電量調查,發現其用電量都在50到350度之間,將用電量的數據繪制成頻率分布直方圖如下.
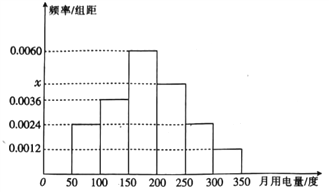
(1)求頻率分布直方圖中![]() 的值并估計這50戶用戶的平均用電量;
的值并估計這50戶用戶的平均用電量;
(2)若將用電量在區間![]() 內的用戶記為
內的用戶記為![]() 類用戶,標記為低用電家庭,用電量在區間
類用戶,標記為低用電家庭,用電量在區間![]() 內的用戶記為
內的用戶記為![]() 類用戶,標記為高用電家庭,現對這兩類用戶進行問卷調查,讓其對供電服務進行打分,打分情況見莖葉圖:
類用戶,標記為高用電家庭,現對這兩類用戶進行問卷調查,讓其對供電服務進行打分,打分情況見莖葉圖:
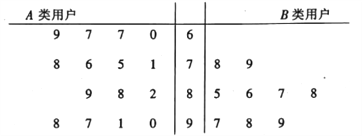
①從![]() 類用戶中任意抽取3戶,求恰好有2戶打分超過85分的概率;
類用戶中任意抽取3戶,求恰好有2戶打分超過85分的概率;
②若打分超過85分視為滿意,沒超過85分視為不滿意,請填寫下面列聯表,并根據列聯表判斷是否有![]() 的把握認為“滿意度與用電量高低有關”?
的把握認為“滿意度與用電量高低有關”?
滿意 | 不滿意 | 合計 | |
| |||
| |||
合計 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
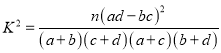 ,
, ![]() .
.
【答案】(1)![]() ,186(2)
,186(2)![]() 沒有
沒有
【解析】試題分析:(1)由矩形面積和為1,求得![]() ,再由每一個矩形的中點橫坐標乘以矩形面積求和可得平均值;
,再由每一個矩形的中點橫坐標乘以矩形面積求和可得平均值;
(2)①![]() 類用戶共9人,打分超過85分的有6人,則
類用戶共9人,打分超過85分的有6人,則![]() 即為所求;
即為所求;
(2)根據數據完成列聯表,利用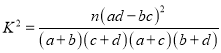 ,計算查表下結論即可.
,計算查表下結論即可.
試題解析:
解:(1)![]()
![]() ,
,
按用電量從低到高的六組用戶數分別為6,9,15,11,6,3,
所以估計平均用電量為![]()
![]() 度.
度.
(2)①![]() 類用戶共9人,打分超過85分的有6人,所以從
類用戶共9人,打分超過85分的有6人,所以從![]() 類用戶中任意抽取3戶,恰好有2戶打分超過85分的概率為
類用戶中任意抽取3戶,恰好有2戶打分超過85分的概率為![]() .
.
②
滿意 | 不滿意 | 合計 | |
| 6 | 9 | 15 |
| 6 | 3 | 9 |
合計 | 12 | 12 | 24 |
因為![]() 的觀測值
的觀測值![]()
![]() ,
,
所以沒有![]() 的把握認為“滿意與否與用電量高低有關”.
的把握認為“滿意與否與用電量高低有關”.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的圖象如圖所示,為了得到g(x)=Acosωx的圖象,只需把y=f(x)的圖象上所有的點( )
)的圖象如圖所示,為了得到g(x)=Acosωx的圖象,只需把y=f(x)的圖象上所有的點( )

A. 向右平移![]() 個單位長度 B. 向左平移
個單位長度 B. 向左平移![]() 個單位長度
個單位長度
C. 向右平移![]() 個單位長度 D. 向左平移
個單位長度 D. 向左平移![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市春節期間7家超市的廣告費支出![]() (萬元)和銷售額
(萬元)和銷售額![]() (萬元)數據如下:
(萬元)數據如下:
超市 | A | B | C | D | E | F | G |
廣告費支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
銷售額 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用線性回歸模型擬合![]() 與
與![]() 的關系,求
的關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)用二次函數回歸模型擬合![]() 與
與![]() 的關系,可得回歸方程:
的關系,可得回歸方程:![]() ,經計算二次函數回歸模型和線性回歸模型的相關指數
,經計算二次函數回歸模型和線性回歸模型的相關指數![]() 分別約為
分別約為![]() 和
和![]() ,請用
,請用![]() 說明選擇哪個回歸模型更合適,并用此模型預測超市應支出多少萬元廣告費,能獲得最大的銷售額?最大的銷售額是多少?(精確到個位數)
說明選擇哪個回歸模型更合適,并用此模型預測超市應支出多少萬元廣告費,能獲得最大的銷售額?最大的銷售額是多少?(精確到個位數)
參數數據及公式:![]() ,
,![]() ,
,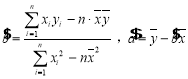 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的上頂點為點
的上頂點為點![]() ,右焦點為
,右焦點為![]() .延長
.延長![]() 交橢圓
交橢圓![]() 于點
于點![]() ,且滿足
,且滿足![]() .
.
(1)試求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 作與
作與![]() 軸不重合的直線
軸不重合的直線![]() 和橢圓
和橢圓![]() 交于
交于![]() 兩點,設橢圓
兩點,設橢圓![]() 的左頂點為點
的左頂點為點![]() ,且直線
,且直線![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點,記直線
兩點,記直線![]() 的斜率分別為
的斜率分別為![]() ,則
,則![]() 與
與![]() 之積是否為定值?若是,求出該定值;若不是,試說明理由.
之積是否為定值?若是,求出該定值;若不是,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雞的產蛋量與雞舍的溫度有關,為了確定下一個時段雞舍的控制溫度,某企業需要了解雞舍的溫度![]() (單位:℃),對某種雞的時段產蛋量
(單位:℃),對某種雞的時段產蛋量![]() (單位:
(單位: ![]() )和時段投入成本
)和時段投入成本![]() (單位:萬元)的影響,為此,該企業收集了7個雞舍的時段控制溫度
(單位:萬元)的影響,為此,該企業收集了7個雞舍的時段控制溫度![]() 和產蛋量
和產蛋量![]() 的數據,對數據初步處理后得到了如圖所示的散點圖和表中的統計量的值.
的數據,對數據初步處理后得到了如圖所示的散點圖和表中的統計量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根據散點圖判斷, ![]() 與
與![]() 哪一個更適宜作為該種雞的時段產蛋量
哪一個更適宜作為該種雞的時段產蛋量![]() 關于雞舍時段控制溫度
關于雞舍時段控制溫度![]() 的回歸方程類型?(給判斷即可,不必說明理由)
的回歸方程類型?(給判斷即可,不必說明理由)
(2)若用![]() 作為回歸方程模型,根據表中數據,建立
作為回歸方程模型,根據表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知時段投入成本![]() 與
與![]() 的關系為
的關系為![]() ,當時段控制溫度為28℃時,雞的時段產蛋量及時段投入成本的預報值分別是多少?
,當時段控制溫度為28℃時,雞的時段產蛋量及時段投入成本的預報值分別是多少?
附:①對于一組具有有線性相關關系的數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]()
![]() 軸,直線
軸,直線![]() 交
交![]() 軸于
軸于![]() 點,
點,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 的面積最大值為1.
的面積最大值為1.
(1)求橢圓![]() 的方程;
的方程;
(2)如圖,過點![]() 作兩條直線與橢圓
作兩條直線與橢圓![]() 分別交于
分別交于![]() ,且使
,且使![]() 軸,問四邊形
軸,問四邊形![]() 的兩條對角線的交點是否為定點?若是,求出該定點的坐標;若不是,請說明理由.
的兩條對角線的交點是否為定點?若是,求出該定點的坐標;若不是,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第47條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”, 《中華人民共和國道路交通安全法》第90條規定:對不禮讓行人的駕駛員處以扣3分,罰款50元的處罰.下表是某市一主干路口監控設備所抓拍的5個月內駕駛員“禮讓斑馬線”行為統計數據:

(1)請利用所給數據求違章人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ,并預測該路口9月份的不“禮讓斑馬線”違章駕駛員人數;
,并預測該路口9月份的不“禮讓斑馬線”違章駕駛員人數;
(2)若從表中1月份和4月份的違章駕駛員中,采用分層抽樣方法抽取一個容量為7的樣本,再從這7人中任選2人進行交規調查,求抽到的兩人恰好來自同一月份的概率.
參考公式: 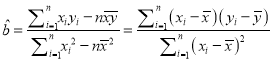 ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com