
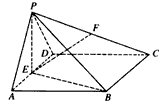
| (Ⅰ)證明:∵E是AD的中點,連結PE, ∴AB=2,AE=1, BE2=AB2+AE2-2AB·AE·cos∠BAD=4+1-2×2×1×cos60°=3, ∴AE2+BE2=1+3=4=AB2, ∴BE⊥AE, 又平面PAD⊥平面ABCD,交線為AD, ∴BE⊥平面PAD. (Ⅱ)證明:取PB中點為H,連接FH,AH, ∵  ,又因為HF是△PBC的中位線, ,又因為HF是△PBC的中位線,∴ 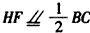 ,∴ ,∴ , ,∴AHFE是平行四邊形, ∴EF∥AH, 又 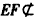 平面PAB,AH 平面PAB,AH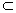 平面PAB, 平面PAB,∴EF∥平面PAB。 (Ⅲ)解:由(Ⅰ)知,BC⊥BE,PE⊥BC, 又PE,BE是平面PBE內兩相交直線, ∴BC⊥平面PBE,又由(Ⅱ)知,HF∥BC, ∴FH⊥平面PBE, ∴∠FEH是直線EF與平面PBE所成的角, 易知, 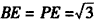 , ,在Rt△PEB中, 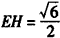 , ,∴ 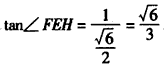 ,∴ ,∴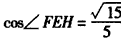 , ,故直線EF與平面PBE所成角的余弦值為 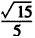 。 。 |
 |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
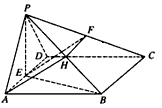
 (2012•武漢模擬)如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,且AD∥BC,∠ABC=90°,側棱PA⊥底面ABCD,若AB=BC=
(2012•武漢模擬)如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,且AD∥BC,∠ABC=90°,側棱PA⊥底面ABCD,若AB=BC=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•河南模擬)如圖,在四棱錐P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E為PD的中點,AB=1,PA=2.
(2012•河南模擬)如圖,在四棱錐P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E為PD的中點,AB=1,PA=2.查看答案和解析>>
科目:高中數學 來源: 題型:
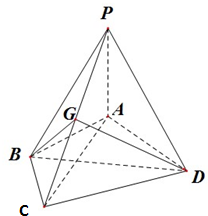 如圖,在四棱錐P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=
如圖,在四棱錐P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=| 7 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年揚州中學) 如圖,在四棱錐P―ABC中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E、F分別為PC、CD的中點
⑴證明:CD⊥平面BEF;
⑵設PA=k?AB,且AD與PC所成的角為60°,求k的值.

查看答案和解析>>
科目:高中數學 來源:2014屆陜西省高一上學期期末考試數學 題型:解答題
(12分)在四棱錐P-ABC中,底面ABCD是矩形,PA 平面ABCD,M,N分別是AB,PC的中點。
平面ABCD,M,N分別是AB,PC的中點。
(1)求證:MN∥平面PAD。
(2)求證:MN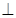 CD.
CD.
(3)若PD與平面ABCD所成的角為450,
求證:MN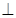 平面PCD.
平面PCD.
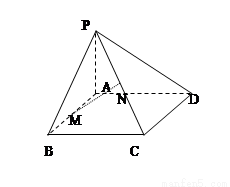
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com