某幼兒園為訓(xùn)練孩子的數(shù)字運(yùn)算能力,在一個(gè)盒子里裝有標(biāo)號(hào)為1,2,3,4,5的卡片各兩張,讓孩子從盒子里任取3張卡片,按卡片上的最大數(shù)字的9倍計(jì)分,每張卡片被取出的可能性都相等,用X表示取出的3張卡片上的最大數(shù)字
(1)求取出的3張卡片上的數(shù)字互不相同的概率;
(2)求隨機(jī)變量X的分布列及數(shù)學(xué)期望;
(3)若孩子取出的卡片的計(jì)分超過(guò)30分,就得到獎(jiǎng)勵(lì),求孩子得到獎(jiǎng)勵(lì)的概率.
【答案】
分析:(1)記事件:“一次取出的3張卡片上的數(shù)字互不相同的事件記為A”,利用古典概型的概率公式可得到結(jié)果.
(2)得到隨機(jī)變量X有可能的取值,計(jì)算出各值對(duì)應(yīng)的概率,列表寫出分布列,代入公式得到數(shù)學(xué)期望.
(3)記事件“一次取卡片所得計(jì)分超過(guò)30分”的事件記為B,看出事件所包含的幾種情況,根據(jù)上面的分布列求和即可.
解答:解:(1)“一次取出的3張卡片上的數(shù)字互不相同”的事件記為A
則
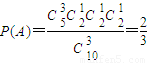
(3分)
(2)變量X的可能取值為2,3,4,5
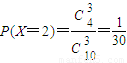
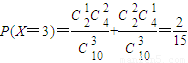
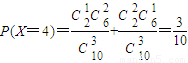
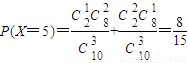
(6分)
所以分布列為
從而E(X)=2×
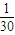
+3×
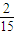
+4×
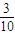
+5×
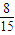
=

(8分)
(3)“一次取卡片所得計(jì)分超過(guò)30分”的事件記為B
∴
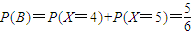
(12分)
∴孩子得到獎(jiǎng)勵(lì)的概率為

(13分)
點(diǎn)評(píng):本題主要考查了離散型隨機(jī)變量的分布列與數(shù)學(xué)期望,以及等可能事件的概率,同時(shí)考查了運(yùn)算求解的能力,屬于中檔題.
科目:高中數(shù)學(xué)
來(lái)源:2012-2013學(xué)年遼寧省本溪一中高三(上)第三次月考數(shù)學(xué)試卷(理科)(解析版)
題型:解答題
某幼兒園為訓(xùn)練孩子的數(shù)字運(yùn)算能力,在一個(gè)盒子里裝有標(biāo)號(hào)為1,2,3,4,5的卡片各兩張,讓孩子從盒子里任取3張卡片,按卡片上的最大數(shù)字的9倍計(jì)分,每張卡片被取出的可能性都相等,用X表示取出的3張卡片上的最大數(shù)字
(1)求取出的3張卡片上的數(shù)字互不相同的概率;
(2)求隨機(jī)變量X的分布列及數(shù)學(xué)期望;
(3)若孩子取出的卡片的計(jì)分超過(guò)30分,就得到獎(jiǎng)勵(lì),求孩子得到獎(jiǎng)勵(lì)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué)
來(lái)源:2012-2013學(xué)年遼寧省本溪一中高三(上)第三次月考數(shù)學(xué)試卷(理科)(解析版)
題型:解答題
某幼兒園為訓(xùn)練孩子的數(shù)字運(yùn)算能力,在一個(gè)盒子里裝有標(biāo)號(hào)為1,2,3,4,5的卡片各兩張,讓孩子從盒子里任取3張卡片,按卡片上的最大數(shù)字的9倍計(jì)分,每張卡片被取出的可能性都相等,用X表示取出的3張卡片上的最大數(shù)字
(1)求取出的3張卡片上的數(shù)字互不相同的概率;
(2)求隨機(jī)變量X的分布列及數(shù)學(xué)期望;
(3)若孩子取出的卡片的計(jì)分超過(guò)30分,就得到獎(jiǎng)勵(lì),求孩子得到獎(jiǎng)勵(lì)的概率.
查看答案和解析>>

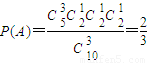 (3分)
(3分)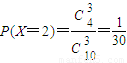
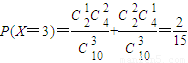
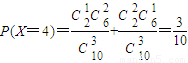
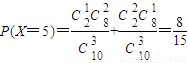 (6分)
(6分)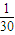
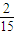
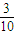
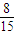
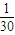 +3×
+3×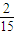 +4×
+4×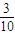 +5×
+5×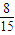 =
= (8分)
(8分)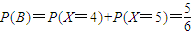 (12分)
(12分) (13分)
(13分)

