
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() .
.
(Ⅰ)討論函數![]() 的單調性;
的單調性;
(Ⅱ)若不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ;當
;當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調減區間為
,單調減區間為![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求出函數的定義域,再求導,根據導數和函數的單調性的關系即可求出,
(Ⅱ)不等式![]() 恒成立轉化為
恒成立轉化為![]() ,則問題轉化為
,則問題轉化為![]() 恒成立時,求
恒成立時,求![]() 的取值范圍,根據導數和函數的單調性的關系即可求出.
的取值范圍,根據導數和函數的單調性的關系即可求出.
(Ⅰ)函數的定義域為![]() ,
,![]() .
.
當![]() 時,
時,![]() ,函數
,函數![]() 在區間
在區間![]() 上是增函數;
上是增函數;
當![]() 時,由
時,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
所以函數![]() 在區間
在區間![]() 上是增函數,在區間
上是增函數,在區間![]() 上是減函數.
上是減函數.
綜上:當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,當
,當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(Ⅱ)不等式![]() .
.
當![]() 時,取
時,取![]() ,
,![]() ,不合題意;
,不合題意;
當![]() 時,令
時,令![]() ,則問題轉化為
,則問題轉化為![]() 恒成立時,求
恒成立時,求![]() 的取值范圍.
的取值范圍.
由于![]() .令
.令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以,函數![]() 的最大值為
的最大值為
![]() ,
,
于是由題意知![]() ,解得
,解得![]() ,
,
故實數![]() 的取值范圍是
的取值范圍是![]() .
.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 的最大值為
的最大值為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(Ⅲ)當![]() 時,令
時,令![]() ,是否存在區間
,是否存在區間![]() .使得函數
.使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() 若存在,求實數
若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 大學就業部從該大學2018年已就業的大學本科畢業生中隨機抽取了100人進行月薪情況的問卷調查,經統計發現,他們的月薪收入在3000元到10000元之間,具體統計數據如表:
大學就業部從該大學2018年已就業的大學本科畢業生中隨機抽取了100人進行月薪情況的問卷調查,經統計發現,他們的月薪收入在3000元到10000元之間,具體統計數據如表:
月薪(百萬) |
|
|
|
|
|
|
|
人數 | 2 | 15 | 20 | 15 | 24 | 10 | 4 |
(1)經統計發現,該大學2018屆的大學本科畢業生月薪![]() (單位:百元)近似地服從正態分布
(單位:百元)近似地服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() (每組數據取區間的中點值).若
(每組數據取區間的中點值).若![]() 落在區間
落在區間![]() 的左側,則可認為該大學本科生屬“就業不理想”的學生,學校將聯系本人,咨詢月薪過低的原因,為以后的畢業生就業提供更好的指導意見.現該校2018屆大學本科畢業生張茗的月薪為3600元,試判斷張茗是否屬于“就業不理想”的學生;
的左側,則可認為該大學本科生屬“就業不理想”的學生,學校將聯系本人,咨詢月薪過低的原因,為以后的畢業生就業提供更好的指導意見.現該校2018屆大學本科畢業生張茗的月薪為3600元,試判斷張茗是否屬于“就業不理想”的學生;
(2)①將樣本的頻率視為總體的概率,若![]() 大學領導決定從
大學領導決定從![]() 大學2018屆所有本畢業生中任意選取5人前去探訪,記這5人中月薪不低于8000元的人數為
大學2018屆所有本畢業生中任意選取5人前去探訪,記這5人中月薪不低于8000元的人數為![]() ,求
,求![]() 的數學期望與方差;
的數學期望與方差;
②在(1)的條件下,中國移動贊助了![]() 大學的這次社會調查活動,并為這次參與調查的大學本科畢業生制定了贈送話費的活動,贈送方式為:月薪低于
大學的這次社會調查活動,并為這次參與調查的大學本科畢業生制定了贈送話費的活動,贈送方式為:月薪低于![]() 的獲贈兩次隨機話費,月薪不低于
的獲贈兩次隨機話費,月薪不低于![]() 的獲贈一次隨機話費;每次贈送的話費及對應的概率分別為:
的獲贈一次隨機話費;每次贈送的話費及對應的概率分別為:
贈送話費(單位:元) | 50 | 100 | 150 |
概率 |
|
|
|
則張茗預期獲得的話費為多少元?(結果保留整數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為建設美麗新農村,某村對本村布局重新進行了規劃,其平面規劃圖如圖所示,其中平行四邊形![]() 區域為生活區,
區域為生活區,![]() 為橫穿村莊的一條道路,
為橫穿村莊的一條道路,![]() 區域為休閑公園,
區域為休閑公園,![]() ,
,![]() ,
,![]() 的外接圓直徑為
的外接圓直徑為![]() .
.

(1)求道路![]() 的長;
的長;
(2)該村準備沿休閑公園的邊界修建柵欄,以防村中的家畜破壞公園中的綠化,試求柵欄總長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]()
(1)求![]() 的軌跡
的軌跡![]()
(2)過軌跡![]() 上任意一點
上任意一點![]() 作圓
作圓![]() 的切線
的切線![]() ,設直線
,設直線![]() 的斜率分別是
的斜率分別是![]() ,試問在三個斜率都存在且不為0的條件下,
,試問在三個斜率都存在且不為0的條件下, 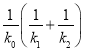 是否是定值,請說明理由,并加以證明.
是否是定值,請說明理由,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業崗位分布條形圖,則下列結論正確的是( )
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.
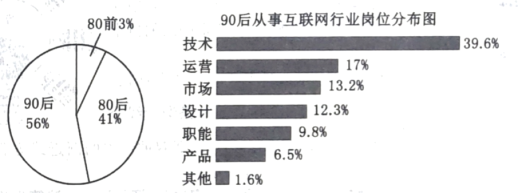
A.互聯網行業從業人員中從事技術和運營崗位的人數占總人數的三成以上
B.互聯網行業中從事技術崗位的人數超過總人數的20%
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com