
已知拋物線![]() :
:![]() 和點
和點![]() ,若拋物線
,若拋物線![]() 上存在不同兩點
上存在不同兩點![]() 、
、![]() 滿足
滿足![]() .
.
(1)求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,拋物線
時,拋物線![]() 上是否存在異于
上是否存在異于![]() 、
、![]() 的點
的點![]() ,使得經過
,使得經過![]() 、
、![]() 、
、![]() 三點的圓和拋物線
三點的圓和拋物線![]() 在點
在點![]() 處有相同的切線,若存在,求出點
處有相同的切線,若存在,求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
(本小題主要考查直線與圓錐曲線等基礎知識,考查數形結合的數學思想方法,以及推理論證能力.運算求解能力)
解法1:(1)不妨設A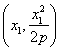 ,B
,B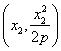 ,且
,且![]() , ∵
, ∵![]() ,∴
,∴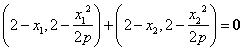 .
.
∴![]() ,
,![]() .…………………4分
.…………………4分
∵![]() (
(![]() ),即
),即![]() ,
,
∴![]() ,即
,即![]() 的取值范圍為
的取值范圍為![]() .…………………6分
.…………………6分
(2)當![]() 時,由(1)求得
時,由(1)求得![]() .
.![]() 的坐標分別為
的坐標分別為![]() .
.![]() .
.
假設拋物線![]() 上存在點
上存在點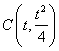 (
(![]() 且
且![]() ),…………8分
),…………8分
使得經過![]() .
.![]() .
.![]() 三點的圓和拋物線
三點的圓和拋物線![]() 在點
在點![]() 處有相同的切線.
處有相同的切線.
設經過![]() .
.![]() .
.![]() 三點的圓的方程為
三點的圓的方程為![]() ,
,
則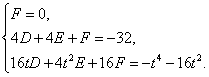
整理得 ![]() . ①…………9分
. ①…………9分
∵函數![]() 的導數為
的導數為![]() ,
,
∴拋物線![]() 在點
在點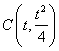 處的切線的斜率為
處的切線的斜率為![]() ,
,
∴經過![]() .
.![]() .
.![]() 三點的圓
三點的圓![]() 在點
在點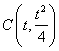 處的切線 斜率為
處的切線 斜率為![]() .………10分
.………10分
∵![]() ,∴直線
,∴直線![]() 的斜率存在.
的斜率存在.
∵圓心![]() 的坐標為
的坐標為![]() ,
,
∴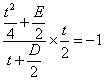 ,
,
即![]() . ②…………………12分
. ②…………………12分
∵![]() ,由①.②消去
,由①.②消去![]() ,得
,得![]() .
.
即![]() .
.
∵![]() ,∴
,∴![]() .
.
故滿足題設的點![]() 存在,其坐標為
存在,其坐標為![]() .…………………14分
.…………………14分
解法2:(1)設![]() ,
,![]() 兩點的坐標為
兩點的坐標為![]() ,且
,且![]() 。
。
∵![]() ,可得
,可得![]() 為
為![]() 的中點,
的中點,
即![]() .…………………2分
.…………………2分
顯然直線![]() 與
與![]() 軸不垂直,
軸不垂直,
設直線![]() 的方程為
的方程為![]() , 即
, 即![]() ,…………………3分
,…………………3分
將![]() 代入
代入![]() 中,
中,
得![]() . …………………4分
. …………………4分
∴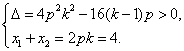 ∴
∴![]() .
.
故![]() 的取值范圍為
的取值范圍為![]() . …………………6分
. …………………6分
(2)當![]() 時,由(1)求得
時,由(1)求得![]() ,
,![]() 的坐標分別為
的坐標分別為![]() .
.
假設拋物線![]() 上存在點
上存在點 (
(![]() 且
且![]() ),
),
使得經過![]() .
.![]() .
.![]() 三點的圓和拋物線
三點的圓和拋物線![]() 在點
在點![]() 處有相同的切線.
處有相同的切線.
設圓的圓心坐標為![]()
![]() ,
,
∵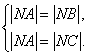
∴ 即
即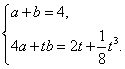 …………………8分
…………………8分
解得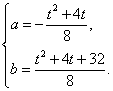 …………………10分
…………………10分
∵拋物線![]() 在點
在點![]() 處切線的斜率為
處切線的斜率為![]() ,
,
而![]() ,且該切線與
,且該切線與![]() 垂直,∴
垂直,∴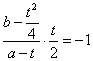 .
.
即![]() . …………………12分
. …………………12分
將![]() ,
,![]() 代入上式,
代入上式,
得![]() .
.
即![]() . ∵
. ∵![]() 且
且![]() ,∴
,∴![]() .
.
故滿足題設的點![]() 存在,其坐標為
存在,其坐標為 ![]() . …………………14分
. …………………14分


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源:2013-2014學年河北省高三上學期四調考試理科數學試卷(解析版) 題型:解答題
如圖,已知拋物線 :
: 和⊙
和⊙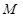 :
: ,過拋物線
,過拋物線 上一點
上一點 作兩條直線與⊙
作兩條直線與⊙ 相切于
相切于 、
、 兩點,分別交拋物線為E、F兩點,圓心點
兩點,分別交拋物線為E、F兩點,圓心點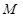 到拋物線準線的距離為
到拋物線準線的距離為 .
.

(Ⅰ)求拋物線 的方程;
的方程;
(Ⅱ)當 的角平分線垂直
的角平分線垂直 軸時,求直線
軸時,求直線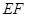 的斜率;
的斜率;
(Ⅲ)若直線 在
在 軸上的截距為,求的最小值.
軸上的截距為,求的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北省高三上學期四調考試文科數學試卷(解析版) 題型:解答題
如圖,已知拋物線 :
: 和⊙
和⊙ :
: ,過拋物線
,過拋物線 上一點
上一點 作兩條直線與⊙
作兩條直線與⊙ 相切于
相切于 、
、 兩點,分別交拋物線為E、F兩點,圓心點
兩點,分別交拋物線為E、F兩點,圓心點 到拋物線準線的距離為
到拋物線準線的距離為 .
.

(1)求拋物線 的方程;
的方程;
(2)當 的角平分線垂直軸時,求直線
的角平分線垂直軸時,求直線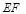 的斜率;
的斜率;
(3)若直線 在
在 軸上的截距為,求的最小值.
軸上的截距為,求的最小值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧沈陽二中等重點中學協作體高三領航高考預測(九)理數學卷(解析版) 題型:解答題
(本小題滿分12分)已知拋物線 :
: 和點
和點 ,若拋物線
,若拋物線 上存在不同兩點
上存在不同兩點 、
、 滿足
滿足 .
.
(I)求實數 的取值范圍;
的取值范圍;
(II)當 時,拋物線
時,拋物線 上是否存在異于
上是否存在異于 的點
的點 ,使得經過
,使得經過 三點的圓和拋物線
三點的圓和拋物線 在點
在點 處有相同的切線,若存在,求出點
處有相同的切線,若存在,求出點 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河北省高三第一次高考仿真測試文科數學試卷(解析版) 題型:解答題
如圖,已知拋物線 :
: 和⊙
和⊙ :
: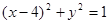 ,過拋物線
,過拋物線 上一點
上一點 作兩條直線與⊙
作兩條直線與⊙ 相切于
相切于 、
、 兩點,分別交拋物線于
兩點,分別交拋物線于 兩點,圓心點
兩點,圓心點 到拋物線準線的距離為
到拋物線準線的距離為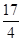 .
.

(Ⅰ)求拋物線 的方程;
的方程;
(Ⅱ)當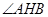 的角平分線垂直
的角平分線垂直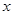 軸時,求直線
軸時,求直線 的斜率;
的斜率;
(Ⅲ)若直線 在
在 軸上的截距為
軸上的截距為 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com